
设![]() 相交于G.,
相交于G.,![]() ,且
,且![]() ,所以
,所以![]() 如图,已知正方体ABCD—A1B1C1D1的棱长为a,求异面直线A1C1与BD1的距离.
如图,已知正方体ABCD—A1B1C1D1的棱长为a,求异面直线A1C1与BD1的距离.
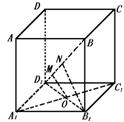
本题的关键是画出A1C1与BD1的公垂线,连B1D1交A1C1于O,在平面BB1D1内作OM⊥BD1,则OM就是A1C1与BD1的公垂线,问题得到解决.
解 连B1D1交A1C1于O,作OM⊥BD1于M.
∴ A1C1⊥B1D1,BB1⊥A1C1,BB1∩B1D1=B1.
∴ A1C1⊥平面BB1D1. ∴ A1C1⊥OM,又OM⊥BD1.
∴ OM是异面直线A1C1与BD1的公垂线.
在直角ΔBB1D1中作B1N⊥BD1于N.
∵ BB1·B1D1=B1N·BD1,a·![]() a=B1N·
a=B1N·![]() a,
a,
∴ B1N=![]() a,OM=
a,OM=![]() B1N=
B1N=![]() a.
a.
故异面直线A1C1与BD1的距离为![]() a.
a.
评析:作异面直线的公垂线一般是比较困难的,只有熟练地掌握线、线垂直,线、面垂直的关系后才能根据题目所给条件灵活作出.本题在求OM的长度时,主要运用中位线和面积的等量关系.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
| OM |
| OA |
| ON |
| OB |
| x |
| x+1 |
| x |
| x+1 |
| 1 |
| f(x) |
| 1 |
| 2 |
| OP |
| OP1 |
| OP2 |
| OPn |
| OP |
| OQ |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 4 |
查看答案和解析>>
科目:高中数学 来源:湖北省荆州中学2008高考复习立体几何基础题题库一(有详细答案)人教版 人教版 题型:044
设A1C与C1O相交于G,∵A1C1∥AC,且A1C1∶OC=2∶1,所以C1O:如图,已知正方体ABCD-A1B1C1D1的棱长为a,求异面直线A1C1与BD1的距离.
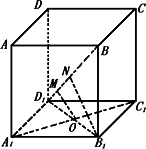
查看答案和解析>>
科目:高中数学 来源: 题型:044
如图,
BC是半圆的直径,D、E是半圆上的两点,且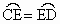 .过C作半圆的切线,与BE的延长线相交于F,BE与CD相交于G,CE、BD的延长线相交于A,连结DE.
.过C作半圆的切线,与BE的延长线相交于F,BE与CD相交于G,CE、BD的延长线相交于A,连结DE.
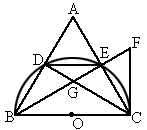
(1)
求证:AB=BC;(2)
如果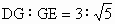 ,BG=3k,试用含k的代数式表示AC;
,BG=3k,试用含k的代数式表示AC;
(3)
设FC=a,BF+FC=b,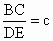 ,求证:
,求证: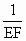 是方程
是方程 的根,并求出这个方程的另一个根.
的根,并求出这个方程的另一个根.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com