
【题目】已知椭圆![]() 的长轴与短轴比值是2,椭圆C过点
的长轴与短轴比值是2,椭圆C过点![]() .
.
(1)求椭圆C的标准方程;
(2)过点![]() 作圆x2+y2=1的切线
作圆x2+y2=1的切线![]() 交椭圆C于A,B两点,记△AOB(O为坐标原点)的面积为S△AOB,将S△AOB表示为m的函数,并求S△AOB的最大值
交椭圆C于A,B两点,记△AOB(O为坐标原点)的面积为S△AOB,将S△AOB表示为m的函数,并求S△AOB的最大值
【答案】(1)![]() (2)
(2)![]() ,m∈(-∞,-1]∪[1,+∞);S△AOB的最大值为1
,m∈(-∞,-1]∪[1,+∞);S△AOB的最大值为1
【解析】
(1) 由已知可知![]() ,及椭圆C过点
,及椭圆C过点![]() ,代入椭圆方程即可求得
,代入椭圆方程即可求得![]() ,进而得出结果.
,进而得出结果.
(2) 由题设知切线![]() 的斜率存在,设切线
的斜率存在,设切线![]() 的方程为
的方程为![]() ,与椭圆方程联立求得弦长
,与椭圆方程联立求得弦长![]() ,由于
,由于![]() 与圆
与圆![]() 相切,可得
相切,可得![]() =1,化简可得
=1,化简可得![]() ,利用基本不等式化简即可求得结果.
,利用基本不等式化简即可求得结果.
解:(1)∵椭圆![]() 的长轴与短轴比值是2,
的长轴与短轴比值是2,
∴![]() ,设椭圆C的方程为:
,设椭圆C的方程为:![]() ,
,
∵椭圆C过点![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴椭圆C的标准方程为![]() .
.
(2)由题意知,![]() .
.
由题设知切线![]() 的斜率存在,设切线
的斜率存在,设切线![]() 的方程为
的方程为![]() ,
,
由 ,得
,得![]() ,
,
设A、B两点的坐标分别为(x1,y1)(x2,y2),
则![]() ,
,
又∵![]() 与圆
与圆![]() 相切,
相切,
∴![]() =1,
=1,![]() ,
,
∴![]() =
=![]()
=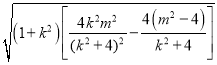
=![]() ,
,
∴![]() ,
,![]()
∴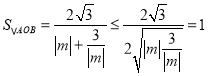 (当且仅当
(当且仅当![]() 时取等号)
时取等号)
∴当![]() 时,S△AOB的最大值为1.
时,S△AOB的最大值为1.


科目:高中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() ,
,![]() 为线段
为线段![]() 的中点(如图1).将
的中点(如图1).将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 的中点(如图2).
的中点(如图2).
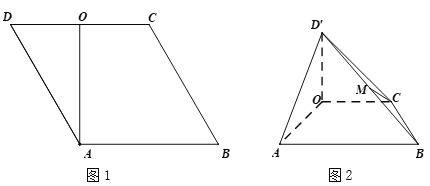
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)当四棱锥![]() 的体积为
的体积为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家规定每年的![]() 月
月![]() 日以后的
日以后的![]() 天为当年的暑假.某钢琴培训机构对
天为当年的暑假.某钢琴培训机构对![]() 位钢琴老师暑假一天的授课量进行了统计,如下表所示:
位钢琴老师暑假一天的授课量进行了统计,如下表所示:
授课量(单位:小时) |
|
|
|
|
|
频数 |
|
|
|
|
|
培训机构专业人员统计近![]() 年该校每年暑假
年该校每年暑假![]() 天的课时量情况如下表:
天的课时量情况如下表:
课时量(单位:天) |
|
|
|
|
|
频数 |
|
|
|
|
|
(同组数据以这组数据的中间值作代表)
(1)估计![]() 位钢琴老师一日的授课量的平均数;
位钢琴老师一日的授课量的平均数;
(2)若以(1)中确定的平均数作为上述一天的授课量.已知当地授课价为![]() 元/小时,每天的各类生活成本为
元/小时,每天的各类生活成本为![]() 元/天;若不授课,不计成本,请依据往年的统计数据,估计一位钢琴老师
元/天;若不授课,不计成本,请依据往年的统计数据,估计一位钢琴老师![]() 天暑假授课利润不少于
天暑假授课利润不少于![]() 万元的概率.
万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市教育局为了监控某校高一年级的素质教育过程,从该校高一年级16个班随机抽取了16个样本成绩,制表如下:
抽取次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
测评成绩 | 95 | 96 | 96 | 90 | 95 | 98 | 98 | 97 |
抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
测评成绩 | 97 | 95 | 96 | 98 | 99 | 96 | 99 | 96 |
令![]() 为抽取的第
为抽取的第![]() 个学生的素质教育测评成绩,
个学生的素质教育测评成绩,![]() ,经计算得,
,经计算得,![]() ,
,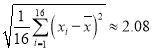 .以下计算精确到0.01.
.以下计算精确到0.01.
(1)设![]() 为抽取的16个样本的成绩,用频率估计概率,求
为抽取的16个样本的成绩,用频率估计概率,求![]() 的分布列、数学期望
的分布列、数学期望![]() 和标准方差
和标准方差![]() ;
;
(2)在抽取的样本成绩中,如果出现了在![]() 之外的成绩,就认为本学期的素质教育过程可能出现了异常情况,需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议.从该校抽样的结果来看,是否需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议?
之外的成绩,就认为本学期的素质教育过程可能出现了异常情况,需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议.从该校抽样的结果来看,是否需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议?
(3)列出不小于![]() 的所有样本成绩,设列出的这些成绩的中位数为
的所有样本成绩,设列出的这些成绩的中位数为![]() ,每次从列出的这些成绩中随机抽取1个成绩,有放回地连续抽取3次,求恰好有2次抽得的成绩为
,每次从列出的这些成绩中随机抽取1个成绩,有放回地连续抽取3次,求恰好有2次抽得的成绩为![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 经过椭圆
经过椭圆![]() :
: ![]() 的左右焦点
的左右焦点![]() ,且与椭圆
,且与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() 三点共线,直线
三点共线,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,且
两点,且![]() (
(![]() ).
).
(1)求椭圆![]() 的方程;
的方程;
(2)当三角形![]() 的面积取得最大值时,求直线
的面积取得最大值时,求直线![]() 的方程.
的方程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com