
【题目】已知圆![]() ,
, ![]() 在抛物线
在抛物线![]() 上,圆
上,圆![]() 过原点且与
过原点且与![]() 的准线相切.
的准线相切.
(Ⅰ) 求![]() 的方程;
的方程;
(Ⅱ) 点![]() ,点
,点![]() (与
(与![]() 不重合)在直线
不重合)在直线![]() 上运动,过点
上运动,过点![]() 作
作![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
, ![]() .求证:
.求证: ![]() (其中
(其中![]() 为坐标原点).
为坐标原点).
【答案】(I)![]() ;(Ⅱ) 见解析.
;(Ⅱ) 见解析.
【解析】试题分析:(I)原点在圆上,抛物线准线与圆相切,可得![]() 三者之间的关系,进而求出
三者之间的关系,进而求出![]() 的方程;(Ⅱ) 设
的方程;(Ⅱ) 设![]() ,
, ![]() ,
, ![]() ,利用导数求得两切线方程,利用根与系数关系可证
,利用导数求得两切线方程,利用根与系数关系可证![]() ,即证两角相等.
,即证两角相等.
试题解析:(I)解法一:因为圆![]() 的圆心在抛物线上且与抛物线的准线相切,且圆半径为
的圆心在抛物线上且与抛物线的准线相切,且圆半径为![]() ,
,
故![]() ,
,
因为圆过原点,所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,所以抛物线
,所以抛物线![]() 方程
方程![]() .
.
解法二:因为圆![]() 的圆心在抛物线上且与抛物线的准线相切,由抛物线的定义,
的圆心在抛物线上且与抛物线的准线相切,由抛物线的定义,
圆![]() 必过抛物线的焦点
必过抛物线的焦点![]() ,
,
又圆![]() 过原点,所以
过原点,所以![]() ,
,
又圆的半径为3,所以![]() ,又
,又![]() ,
,
又![]() ,得
,得![]() ,所以
,所以![]() .所以抛物线
.所以抛物线![]() 方程
方程![]() .
.
解法三:因为圆![]() 与抛物线准线相切,所以
与抛物线准线相切,所以![]() ,
,
且圆过![]() 又圆过原点,故
又圆过原点,故![]() ,可得
,可得![]() ,
,
解得![]() ,所以抛物线
,所以抛物线![]() 方程
方程![]()
(Ⅱ) 解法一:设![]() ,
, ![]() ,
, ![]() ,
, ![]() 方程为
方程为![]() ,所以
,所以![]() , 5分
, 5分
求得抛物线在点![]() 处的切线的斜率
处的切线的斜率![]() ,所以切线
,所以切线![]() 方程为:
方程为: ![]() ,
,
即![]() ,化简得
,化简得![]() ,
,
又因过点![]() ,故可得,
,故可得, ![]() ,
,
即![]() ,同理可得
,同理可得![]() ,
,
所以![]() 为方程
为方程![]() 的两根,所以
的两根,所以![]() ,
, ![]() ,
,
因为![]() ,所以
,所以![]() ,
,
化简![]()
![]() .
.
所以![]() .
.
解法二:依题意设点![]() ,设过点
,设过点![]() 的切线为
的切线为![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,即
,即![]() ,
,
不妨设切线![]() 的斜率为
的斜率为![]() ,点
,点![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,又
,又![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ,
, ![]() ,即点
,即点![]() ,同理点
,同理点![]() ,
,
因为![]() ,所以
,所以![]() ,同理
,同理![]() ,
,
所以
![]()
![]() ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】棉花的纤维长度是评价棉花质量的重要指标,某农科所的专家在土壤环境不同的甲、乙两块实验地分别种植某品种的棉花,为了评价该品种的棉花质量,在棉花成熟后,分别从甲、乙两地的棉花中各随机抽取20根棉花纤维进行统计,结果如下表:(记纤维长度不低于300![]() 的为“长纤维”,其余为“短纤维”)
的为“长纤维”,其余为“短纤维”)
纤维长度 |
|
|
|
|
|
甲地(根数) | 3 | 4 | 4 | 5 | 4 |
乙地(根数) | 1 | 1 | 2 | 10 | 6 |
(1)由以上统计数据,填写下面![]() 列联表,并判断能否在犯错误概率不超过0.025的前提下认为“纤维长度与土壤环境有关系”.
列联表,并判断能否在犯错误概率不超过0.025的前提下认为“纤维长度与土壤环境有关系”.
甲地 | 乙地 | 总计 | |
长纤维 | |||
短纤维 | |||
总计 |
附:(1) ;
;
(2)临界值表;
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)现从上述40根纤维中,按纤维长度是否为“长纤维”还是“短纤维”采用分层抽样的方法抽取8根进行检测,在这8根纤维中,记乙地“短纤维”的根数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn , 若对于任意的正整数n都有Sn=2an﹣3n.
(1)设bn=an+3,求证:数列{bn}是等比数列,并求出{an}的通项公式;
(2)求数列{nan}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长沙市物价监督部门为调研某公司新开发上市的一种产品销售价格的合理性,对某公司的该产品的销量与价格进行了统计分析,得到如下数据和散点图:
定价 | 10 | 20 | 30 | 40 | 50 | 60 |
年销量 | 1150 | 643 | 424 | 262 | 165 | 86 |
| 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |

(参考数据: ![]() ,
,
![]() )
)
(1)根据散点图判断, ![]() 与
与![]() 和
和![]() 与
与![]() 哪一对具有的线性相关性较强(给出判断即可,不必说明理由)?
哪一对具有的线性相关性较强(给出判断即可,不必说明理由)?
(2)根据(1)的判断结果及数据,建立![]() 关于
关于![]() 的回归方程(方程中的系数均保留两位有效数字).
的回归方程(方程中的系数均保留两位有效数字).
(3)定价为多少元/ ![]() 时,年销售额的预报值最大?
时,年销售额的预报值最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C方程为 ![]() (a>b>0),左、右焦点分别是F1 , F2 , 若椭圆C上的点P(1,
(a>b>0),左、右焦点分别是F1 , F2 , 若椭圆C上的点P(1, ![]() )到F1 , F2的距离和等于4. (Ⅰ)写出椭圆C的方程和焦点坐标;
)到F1 , F2的距离和等于4. (Ⅰ)写出椭圆C的方程和焦点坐标;
(Ⅱ)设点Q是椭圆C的动点,求线段F1Q中点T的轨迹方程;
(Ⅲ)直线l过定点M(0,2),且与椭圆C交于不同的两点A,B,若∠AOB为锐角(O为坐标原点),求直线l的斜率k0的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() :
: ![]() ,曲线
,曲线![]() :
: ![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(Ⅰ)求曲线![]() ,
, ![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)曲线![]() :
: ![]() (
(![]() 为参数,
为参数, ![]() ,
, ![]() )分别交
)分别交![]() ,
, ![]() 于
于![]() ,
, ![]() 两点,当
两点,当![]() 取何值时,
取何值时, ![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
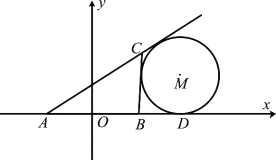
【题目】如图所示,在![]() 中,
中, ![]() 的中点为
的中点为![]() ,且
,且![]() ,点
,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .固定边
.固定边![]() ,在平面内移动顶点
,在平面内移动顶点![]() ,使得圆
,使得圆![]() 与边
与边![]() ,边
,边![]() 的延长线相切,并始终与
的延长线相切,并始终与![]() 的延长线相切于点
的延长线相切于点![]() ,记顶点
,记顶点![]() 的轨迹为曲线
的轨迹为曲线![]() .以
.以![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 为坐标原点如图所示建立平面直角坐标系.
为坐标原点如图所示建立平面直角坐标系.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)设动直线![]() 交曲线
交曲线![]() 于
于![]() 两点,且以
两点,且以![]() 为直径的圆经过点
为直径的圆经过点![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a1=3,an=2an﹣1+(t+1)2n+3m+t(t,m∈R,n≥2,n∈N*)
(1)t=0,m=0时,求证: ![]() 是等差数列;
是等差数列;
(2)t=﹣1,m= ![]() 是等比数列;
是等比数列;
(3)t=0,m=1时,求数列{an}的通项公式和前n项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com