
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() .
.
(1)证明![]() 是等差数列,并求
是等差数列,并求![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() ,
,![]() ,记
,记![]() 表示不超过x的最大整数,求关于n的不等式
表示不超过x的最大整数,求关于n的不等式 的解集.
的解集.
【答案】(1)证明见解析; ![]() (2)
(2)![]()
【解析】
(1)根据等差数列定义,求得![]() 是常数即可证明
是常数即可证明![]() 为等差数列;由累加法,可求得数列
为等差数列;由累加法,可求得数列![]() 的通项公式.
的通项公式.
(2)由![]() 代入
代入![]() 的通项公式中求得
的通项公式中求得![]() ,同取倒数后可得
,同取倒数后可得![]() ,结合裂项法求和可得
,结合裂项法求和可得![]() .判断出
.判断出![]() 的单调性,即可求得
的单调性,即可求得![]() 的值域,即可求得
的值域,即可求得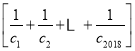 的值.再解关于
的值.再解关于![]() 的不等式,即可求得正整数
的不等式,即可求得正整数![]() 的值,即为不等式的解集.
的值,即为不等式的解集.
(1)数列![]() 满足
满足![]() ,数列
,数列![]() 满足
满足![]()
则![]()
![]()
且![]() ,
,![]()
所以数列![]() 是以
是以![]() 为首项,公差为2的等差数列
为首项,公差为2的等差数列
则![]()
即![]()
利用递推公式可得
![]()
![]()
![]()
![]()
![]()
![]()
![]()
等式两边分别相加可得![]()
而![]()
所以![]()
因为![]() 也满足上式
也满足上式
所以![]()
(2)数列![]() 满足
满足![]()
则![]()
同取倒数可得![]()
即![]()
所以![]()
![]()
![]()
而![]()
所以![]()
由![]()
可得![]()
所以![]()
所以![]()
所以![]()
则![]()
所以由定义可得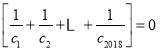
则不等式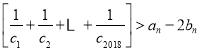 等价于
等价于![]()
而由(1)可知,![]() ,
,![]()
所以![]()
解得![]() ,又
,又![]()
所以![]()
所以关于n的不等式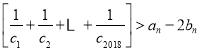 的解集为
的解集为![]()


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上.

(Ⅰ)求证:EF⊥平面PAC;
(Ⅱ)若M为PD的中点,求证:ME∥平面PAB;
(Ⅲ)如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图,则下列结论中不一定正确的是( )

A. 互联网行业从业人员中90后占一半以上
B. 互联网行业中从事技术岗位的人数超过总人数的![]()
C. 互联网行业中从事运营岗位的人数90后比80前多
D. 互联网行业中从事运营岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方形的边长为![]() 分别为
分别为![]() 的中点,以
的中点,以![]() 为棱将正方形
为棱将正方形![]() 折成如图所示的
折成如图所示的![]() 的二面角,点
的二面角,点![]() 在线段
在线段![]() 上.
上.

(1)若![]() 为
为![]() 的中点,且直线
的中点,且直线![]() ,由
,由![]() 三点所确定平面的交点为
三点所确定平面的交点为![]() ,试确定点
,试确定点![]() 的位置,并证明直线
的位置,并证明直线![]() 平面
平面![]() ;
;
(2)是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ;若存在,求此时二面角
;若存在,求此时二面角![]() 的余弦值,若不存在,说明理由.
的余弦值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
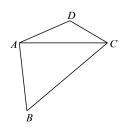
【题目】我国南宋著名数学家秦九韶(约1202—1261)被国外科学史家赞誉为“他那个民族,那个时代,并且确实也是所有时代最伟大的数学家之一”.他独立推出了“三斜求积”公式,求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实.一为从隅,开平方得积.”把以上这段文字写成从三条边长求三角形面积的公式,就是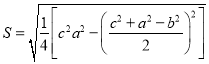 .现如图,已知平面四边形
.现如图,已知平面四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则平面四边形
,则平面四边形![]() 的面积是_________.
的面积是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中装有9张各写有一个数字的卡片,其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3.从盒中任取3张卡片.
(1)求所取3张卡片上的数字完全相同的概率;
(2)X表示所取3张卡片上的数字的中位数,求![]() 的分布列.
的分布列.
(注:若三个数![]() ,
,![]() ,
,![]() 满足
满足![]() ,则称
,则称![]() 为这三个数的中位数)
为这三个数的中位数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com