【题目】下列命题为真命题的是（ ）
A.若
为真命题，则
为真命题；
B.“
”是“
”的充分不必要条件；
C.命题“若
，则
”的否命题为“若，则
”；
D.已知命题
，使得
，则
，使得
。
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】如图是一个“蝴蝶形图案（阴影区域）”，其中
是过抛物线
的两条互相垂直的弦（点
在第二象限），且交于点
，点
为
轴上一点，
，其中
为锐角
（1）设线段
的长为
，将表示为关于的函数
（2）求“蝴蝶形图案”面积的最小值，并指出取最小值时的大小
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知定义域为
的函数
在
上有最大值1，设
．
（1）求
的值；
（2）若不等式
在
上恒成立，求实数
的取值范围；
（3）若函数
有三个不同的零点，求实数的取值范围（
为自然对数的底数）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知指数函数
的图象经过点
，
在区间
的最小值
；
（1）求函数的解析式；
（2）求函数
的最小值的表达式；
（3）是否存在
同时满足以下条件:①
；②当的定义域为
时，值域为
；若存在，求出m，n的值；若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，BC边上的高所在直线的方程为x+2y+3=0，∠A的平分线所在直线的方程为y=0，若点B的坐标为（﹣1，﹣2），分别求点A和点C的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学有初中学生1800人，高中学生1200人.为了解全校学生本学期开学以来的课外阅读时间，学校采用分层抽样方法，从中抽取了100名学生进行问卷调查.将样本中的“初中学生”和“高中学生”，按学生的课外阅读时间(单位：小时)各分为5组：
，
，
，
，
，得其频率分布直方图如图所示.
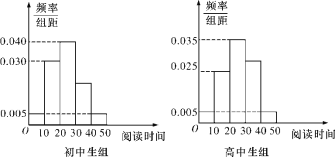
（1）估计全校学生中课外阅读时间在小时内的总人数约是多少；
（2）从全校课外阅读时间不足10个小时的样本学生中随机抽取3人，求至少有2个初中生的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】己知抛物线
的顶点为
,与
轴的交点为
,则直线
称为抛物线
的伴随直线.
(1)求抛物线
的伴随直线的表达式;
(2)已知抛物线
的伴随直线为
,且该抛物线与
轴有两个不同的公共点,求
的取值范围.
(3)已知
,若抛物线的伴随直线为
,且该抛物线与线段
恰有1个公共点,求的取值范围(直接写出答案即可)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
为双曲线
的左、右焦点，过
作垂直于
轴的直线，并在轴上方交双曲线于点
，且
.
（1）求双曲线
的方程；
（2）过双曲线上一点
作两条渐近线的垂线，垂足分别是
和
，试求
的值；
（3）过圆
上任意一点
作切线
交双曲线于
两个不同点，
中点为
，证明：
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】据不完全统计，某厂的生产原料耗费
（单位：百万元）与销售额
（单位：百万元）如下：
| 2 | 4 | 6 | 8 |
| 30 | 40 | 50 | 70 |
变量、为线性相关关系.
（1）求线性回归方程必过的点；
（2）求线性回归方程；
（3）若实际销售额要求不少于
百万元，则原材料耗费至少要多少百万元。
，
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
