
已知函数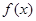 是R上的单调增函数且为奇函数,数列
是R上的单调增函数且为奇函数,数列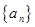 是等差数列,
是等差数列,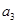 >0,则
>0,则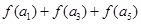 的值 ( )
的值 ( )
A.恒为正数 B.恒为负数 C.恒为0 D.可正可负
A
【解析】
试题分析:∵函数f(x)是R上的奇函数且是增函数数列,
∴取任何x2>x1,总有f(x2)>f(x1)。
∵函数f(x)是R上的奇函数,∴f(0)=0,
∵函数f(x)是R上的奇函数且是增函数,
∴当x>0,f(0)>0,
当x<0,f(0)<0.
∵数列{an}是等差数列,
a1+a5=2a3, a3>0,∴a1+a5>0,
则f(a1)+f(a5)>0,
∵f(a3)>0,
∴f(a1)+f(a3)+f(a5)恒为正数,故选A。
考点:本题主要考查函数的奇偶性、单调性,等差数列的性质。
点评:中档题,本题综合应用函数奇偶性及单调性,逐步确定得到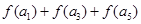 满足的条件。有一定综合性,较为典型。
满足的条件。有一定综合性,较为典型。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2011-2012学年广东省广州市高三上学期第3次月考理科数学试卷(解析版) 题型:选择题
已知函数 是R上的单调增函数且为奇函数,数列
是R上的单调增函数且为奇函数,数列 是等差数列,
是等差数列, >0,则
>0,则 的值
( )
的值
( )
A.恒为正数 B.恒为负数
C.恒为0 D.可以为正数也可以为负数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com