练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在△ABC中，角A，B，C的对边分别为a，b，c，若b（tanA+tanB）= ctanB，BC边的中线长为1，则a的最小值为 ．

    【答案】2 -2
    【解析】解：在△ABC中，∵b（tanA+tanB）= ctanB，∴b（ ）= ， ∴bsinC= csinBcosA，
    ∴bc= bccosA，∴cosA= ．
    ∵BC边的中线长为1，∴ =2，
    ∴c2+b2+2bccosA=4，即b2+c2=4﹣ bc≥2bc，解得bc≤4﹣2 ．
    ∴a2=（ ）2=b2+c2﹣2bccosA=4﹣2 bc≥4﹣2 （4﹣2 ）=12﹣8 ．
    ∴a的最小值为 =2 ﹣2．
    所以答案是：2 -2．
    【考点精析】根据题目的已知条件，利用正弦定理的定义的相关知识可以得到问题的答案，需要掌握正弦定理:．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足：an+1+（﹣1）nan=n+2（n∈N*），则S20=（ ）
    A.130
    B.135
    C.260
    D.270

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： =1（a＞b＞0）的离心率为 ，且经过点（1， ），F1 ， F2是椭圆的左、右焦点．
    （1）求椭圆C的方程；
    （2）点P在椭圆上运动，求|PF1||PF2|的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设等差数列{an}前n项和为Sn ， 且满足a2=2，S5=15；等比数列{bn}满足b2=4，b5=32．
    （1）求数列{an}、{bn}的通项公式；
    （2）求数列{anbn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）同时满足①f（x）为偶函数；②对任意x，有f（ ﹣x）=f（ +x），则函数f（x）的解析式可以是（ ）
    A.f（x）=cos2x
    B.
    C.f（x）=cos6x
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足an+1=λan+2n（n∈N* ， λ∈R），且a1=2．
    （1）若λ=1，求数列{an}的通项公式；
    （2）若λ=2，证明数列{ }是等差数列，并求数列{an}的前n项和Sn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知三条直线l1：ax﹣y+a=0，l2：x+ay﹣a（a+1）=0，l3：（a+1）x﹣y+a+1=0，a＞0．
    （1）证明：这三条直线共有三个不同的交点；
    （2）求这三条直线围成的三角形的面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将一颗质地均匀的正方体骰子（六个面的点数分别为1，2，3，4，5，6）先后抛掷两次，记第一次出现的点数为x，第二次出现的点数为y．
    （1）求事件“x+y≤3”的概率；
    （2）求事件“|x﹣y|=2”的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形ABCD和ADPQ均为正方形，他们所在的平面互相垂直，动点M在线段PQ上，E、F分别为AB、BC的中点，设异面直线EM与AF所成的角为θ，则cosθ的最大值为 ．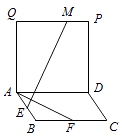

    查看答案和解析>>

    同步练习册答案