
已知数列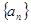 满足:
满足: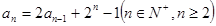 且
且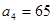 .(1)求数列
.(1)求数列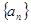 的前三项;(2)是否存在一个实数
的前三项;(2)是否存在一个实数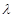 ,使数列
,使数列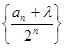 为等差数列?若存在,求出
为等差数列?若存在,求出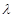 的值;若不存在,说明理由;(3)求数列
的值;若不存在,说明理由;(3)求数列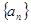 的前
的前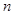 项和
项和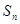 .
.
(1) 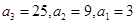 (2)
(2)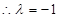 时,
时,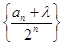 成等差数列
成等差数列
(3)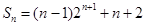
【解析】
试题分析:本题第(1)问,直接根据条件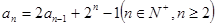 ,取n=1,2,3,代入即可求解;
,取n=1,2,3,代入即可求解;
第(2)问,先假设其存在,然后根据等差数列对应的相邻两项的差为常数即可求出λ的值;
第(3)问,先根据条件求出数列{an}的通项公式,再借助于分组求和以及错位相减求和即可求出结论.
解:(1)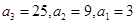
(2)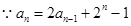
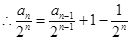 ,
,
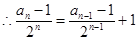
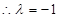 时,
时,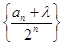 成等差数列
成等差数列
(3) 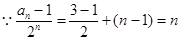
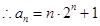
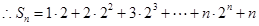
令 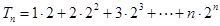
则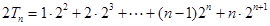
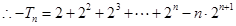
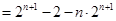
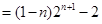
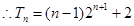
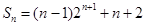
考点:数列递推式;等差关系的确定;数列的求和.
点评:本题主要考察利用数列的递推式求数列的特定项以及数列的求和问题.本题涉及到数列求和的分组法以及错位相减法,错位相减法适用于一等差数列与一等比数列相乘组成的新数列.


科目:高中数学 来源:2010-2011学年江苏省溱潼中学高二年级期中数学(理)试卷(一) 题型:解答题
已知数列 满足
满足 ,且
,且 (
( )
)
(1)求 ,
, ,
, (2)由(1)猜想
(2)由(1)猜想 的通项公式
的通项公式 ;
;
(3)用数学归纳法证明(2)的结果。
查看答案和解析>>
科目:高中数学 来源:2010年哈三中高二下学期期末测试数学理 题型:解答题
(本小题满分12分)
已知数列 满足
满足 ,且
,且 (
( )。
)。
(1) 求 、
、 、
、 的值;
的值;
(2) 猜想数列 的通项公式,并用数学归纳法加以证明。
的通项公式,并用数学归纳法加以证明。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年黑龙江省高三第三次模拟考试理科数学试卷(解析版) 题型:解答题
已知数列 满足
满足 ,且
,且 (n
(n 2且n∈N*).
2且n∈N*).
(Ⅰ)求数列 的通项公式;(5分)
的通项公式;(5分)
(Ⅱ)设数列 的前n项之和
的前n项之和 ,求
,求 ,并证明:
,并证明: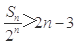 .(7分)
.(7分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com