
(2007
山东,22)设函数 ,其中b≠0.
,其中b≠0.
(1)
当 时,判断函数f(x)在定义域上的单调性;
时,判断函数f(x)在定义域上的单调性;
(2)
求函数f(x)的极值点;(3)
证明对任意的正整数n,不等式 都成立.
都成立. |
解析: (1)由题意知,f(x)的定义域为(―1,+∞),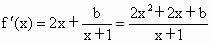 , ,
设 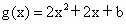 ,其图象的对称轴为 ,其图象的对称轴为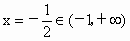 , ,
∴ 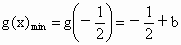 .当 .当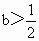 时, 时,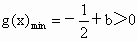 . .
即 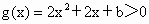 在(―1,+∞)上恒成立. 在(―1,+∞)上恒成立.
∴当 x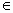 (―1,+∞)时, (―1,+∞)时,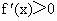 . .
∴当 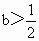 时,函数f(x)在定义域(―1,+∞)上单调递增. 时,函数f(x)在定义域(―1,+∞)上单调递增.
(2) ①由(1)得:当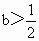 时,函数f(x)无极值点. 时,函数f(x)无极值点.
② 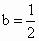 时, 时,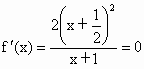 有两个相同的解 有两个相同的解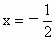 , ,
∵ 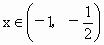 时, 时,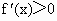 , ,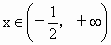 时, 时,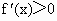 , ,
∴ 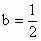 时,函数f(x)在(―1,+∞)上无极值点. 时,函数f(x)在(―1,+∞)上无极值点.
③当 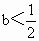 时, 时, 有两个不同解, 有两个不同解,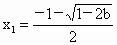 , , . .
∵ b<0时,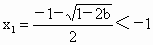 , ,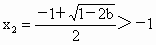 , ,
即 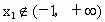 , ,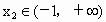 , ,
∴ b<0时,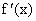 、f(x)随x的变化情况如下表: 、f(x)随x的变化情况如下表:
由此表可知 b<0时,f(x) 有唯一极小值点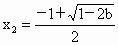 ;当 ;当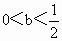 时, 时,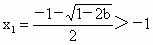 ,∴ ,∴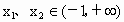 , ,
此时, 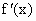 、f(x)随x的变化情况如下表: 、f(x)随x的变化情况如下表:
由此表可知: 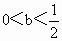 时,f(x)有一个极大值点 时,f(x)有一个极大值点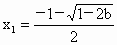 和一个极小值点 和一个极小值点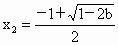 ; ;
综上所述, b<0时,f(x)有唯一极小值点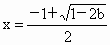 ; ;
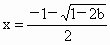 和一个极小值点 和一个极小值点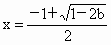 ; ;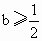 时,f(x)无极值点. 时,f(x)无极值点.
(3) 当b=-1时,函数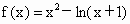 ,令函数 ,令函数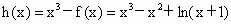 ,则 ,则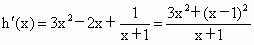 .∴当x .∴当x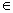 [0,+∞)时, [0,+∞)时,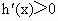 ,所以函数h(x)在[0,+∞)上单调递增,又h(0)=0,∴x ,所以函数h(x)在[0,+∞)上单调递增,又h(0)=0,∴x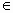 [0,+∞)时,恒有h(x)>h(0)=0,即 [0,+∞)时,恒有h(x)>h(0)=0,即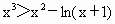 恒成立,故当x 恒成立,故当x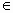 [0,+∞)时,有 [0,+∞)时,有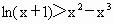 .对任意正整数n,取 .对任意正整数n,取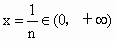 ,则有 ,则有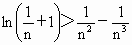 ,所以结论成立. ,所以结论成立. |


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com