
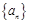 是首项为1,公差为
是首项为1,公差为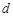 的等差数列,数列
的等差数列,数列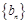 是首项为1,公比为
是首项为1,公比为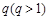 的等比
的等比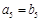 ,
,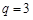 ,求数列
,求数列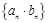 的前
的前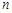 项和;
项和;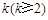 ,使得
,使得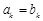 .试比较
.试比较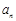 与
与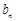 的大小,并说明理由.
的大小,并说明理由.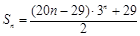 ;(2) 当
;(2) 当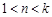 时,
时,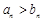 ;当
;当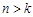 时,
时,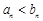 ;当
;当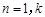 时,
时,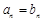 .
.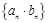 的前
的前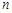 项和;(2)利用
项和;(2)利用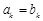 等量关系关系,减少公差d,进而将
等量关系关系,减少公差d,进而将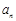 与
与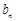 进行表示,然后才有作差比较进行分析,注意分类讨论思想的应用.
进行表示,然后才有作差比较进行分析,注意分类讨论思想的应用.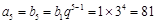 ,
, ,
,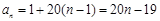 , 3分
, 3分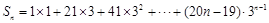 , ①
, ① , ②
, ②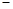 ②得,
②得,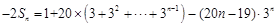 ,
,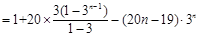
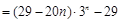 ,
,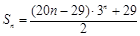 . 7分
. 7分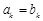 ,
,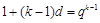 ,即
,即 ,
, ,
,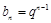 , 9分
, 9分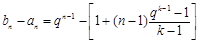
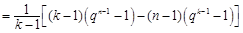
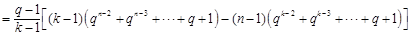
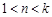 时,由
时,由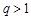 知
知
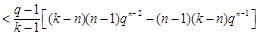
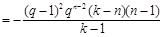
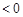 , 13分
, 13分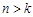 时,由
时,由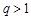 知
知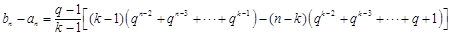
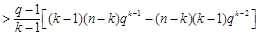
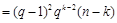
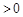 ,
,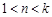 时,
时,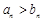 ;当
;当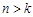 时,
时,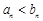 ;当
;当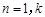 时,
时,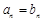 . 16分
. 16分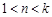 时,
时,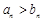 ;
;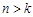 时,
时,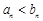 ”得2分.)
”得2分.)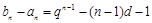 (易知
(易知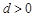 ),
),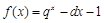 ,有
,有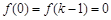 ,
,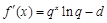 ,
,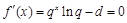 ,则
,则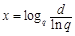 .记
.记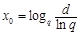 .
.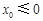 ,则在
,则在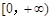 上
上 ,函数
,函数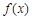 在
在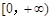 上为单调增函数,则
上为单调增函数,则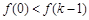 ,
,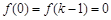 相矛盾;
相矛盾;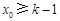 ,则在
,则在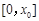 上
上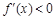 ,函数
,函数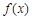 在
在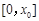 上为单调减函数,则
上为单调减函数,则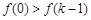 ,
,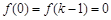 相矛盾;
相矛盾; .
.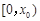 上
上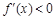 ,函数
,函数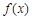 在
在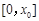 上为单调减函数,
上为单调减函数,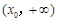 上
上 ,函数
,函数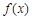 在
在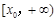 上为单调增函数.
上为单调增函数.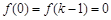 ,所以,当
,所以,当 时,
时,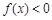 ,当
,当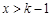 时,
时,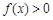 ,
,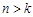 时,
时,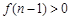 ,即
,即 ,
,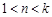 时,
时,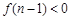 ,即
,即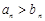 ,
,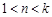 时,
时,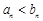 ;当
;当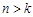 时,
时,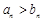 ;当
;当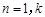 时,
时,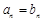 .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com