
如图,四棱锥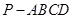 中,四边形
中,四边形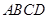 为矩形,
为矩形,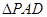 为等腰三角形,
为等腰三角形,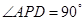 ,平面
,平面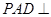 平面
平面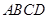 ,且
,且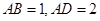 ,
,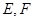 分别为
分别为 和
和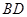 的中点.
的中点.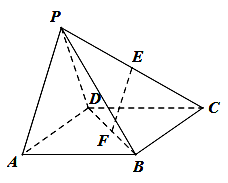
(Ⅰ)证明: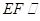 平面
平面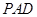 ;
;
(Ⅱ)证明:平面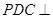 平面
平面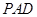 ;
;
(Ⅲ)求四棱锥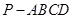 的体积.
的体积.
(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)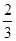 .
.
解析试题分析:(Ⅰ)证明线面平行,一般可考虑线面平行的判定定理,构造面外线平行于面内线,其手段一般是构造平行四边形,或构造三角形中位线(特别是有中点时),本题易证 从而达到目标;(Ⅱ)要证面面垂直,由面面垂直的判定定理知可先考察线面垂直,要证线面垂直,又要先考察线线垂直;(Ⅲ)求棱锥的体积,关键是作出其高,由面
从而达到目标;(Ⅱ)要证面面垂直,由面面垂直的判定定理知可先考察线面垂直,要证线面垂直,又要先考察线线垂直;(Ⅲ)求棱锥的体积,关键是作出其高,由面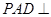 面
面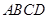 及
及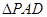 为等腰直角三角形,易知
为等腰直角三角形,易知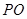 (
(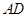 中点为
中点为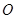 ),就是其高,问题得以解决.
),就是其高,问题得以解决.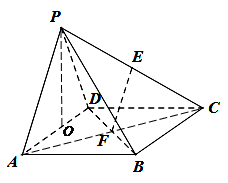
试题解析:(Ⅰ)证明:如图,连结 .
.
∵四边形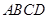 为矩形且
为矩形且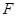 是
是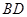 的中点.∴
的中点.∴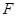 也是
也是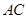 的中点.
的中点.
又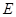 是
是 的中点,
的中点, 2分
2分
∵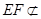 平面
平面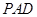 ,
,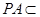 平面
平面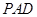 ,所以
,所以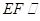 平面
平面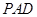 ; 4分
; 4分
(Ⅱ)证明:∵平面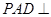 平面
平面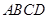 ,
,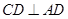 ,平面
,平面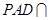 平面
平面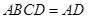 ,
,
所以平面 平面
平面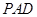 ,又
,又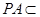 平面
平面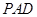 ,所以
,所以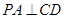 6分
6分
又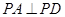 ,
,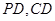 是相交直线,所以
是相交直线,所以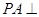 面
面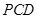
又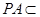 平面
平面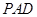 ,平面
,平面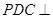 平面
平面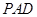 ; 8分
; 8分
(Ⅲ)取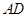 中点为
中点为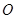 .连结
.连结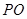 ,
,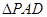 为等腰直角三角形,所以
为等腰直角三角形,所以 ,
,
因为面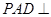 面
面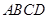 且面
且面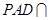 面
面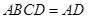 ,
,
所以,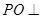 面
面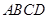 ,
,
即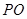 为四棱锥
为四棱锥 的高.
的高.  10分
10分
由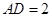 得
得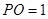 .又
.又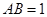 .
.
∴四棱锥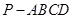 的体积
的体积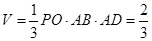 12分
12分
考点:空间中线面的位置关系、空间几何体的体积.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:解答题
如图所示,在正方体ABCD﹣A1B1C1D1中,棱长AB=1.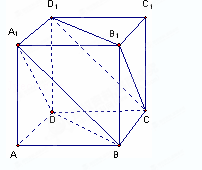
(Ⅰ)求异面直线A1B与 B1C所成角的大小;(Ⅱ)求证:平面A1BD∥平面B1CD1.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD为平行四边形,其中AB=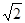 , BD=BC=1, AA1=2,E为DC的中点,F是棱DD1上的动点.
, BD=BC=1, AA1=2,E为DC的中点,F是棱DD1上的动点.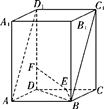
(1)求异面直线AD1与BE所成角的正切值;
(2)当DF为何值时,EF与BC1所成的角为90°?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,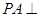 平面
平面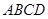 ,四边形
,四边形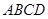 是矩形,
是矩形,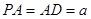 ,M,N分别是AB,PC的中点,
,M,N分别是AB,PC的中点,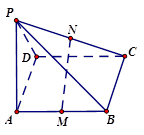
(1)求平面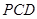 和平面
和平面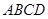 所成二面角的大小,
所成二面角的大小,
(2)求证: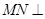 平面
平面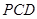
(3)当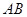 的长度变化时,求异面直线PC与AD所成角的可能范围.
的长度变化时,求异面直线PC与AD所成角的可能范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四棱锥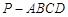 中,底面
中,底面 为直角梯形,
为直角梯形, ∥
∥ ,
,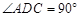 ,平面
,平面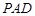 ⊥底面
⊥底面 ,
,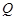 为
为 的中点,
的中点, 是棱
是棱 上的点,
上的点,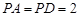 ,
,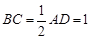 ,
,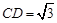 .
.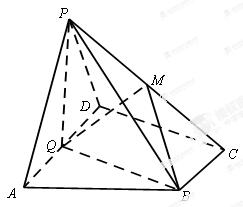
(Ⅰ)求证:平面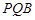 ⊥平面
⊥平面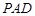 ;
;
(Ⅱ)若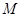 为棱
为棱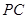 的中点,求异面直线
的中点,求异面直线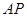 与
与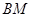 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com