
【题目】如图,湖中有一个半径为![]() 千米的圆形小岛,岸边点
千米的圆形小岛,岸边点![]() 与小岛圆心
与小岛圆心![]() 相距
相距![]() 千米,为方便游人到小岛观光,从点
千米,为方便游人到小岛观光,从点![]() 向小岛建三段栈道
向小岛建三段栈道![]() ,
,![]() ,
,![]() ,湖面上的点
,湖面上的点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() 均与圆
均与圆![]() 相切,切点分别为
相切,切点分别为![]() ,
,![]() ,其中栈道
,其中栈道![]() ,
,![]() ,
,![]() 和小岛在同一个平面上.沿圆
和小岛在同一个平面上.沿圆![]() 的优弧(圆
的优弧(圆![]() 上实线部分)上再修建栈道
上实线部分)上再修建栈道![]() .记
.记![]() 为
为![]() .
.
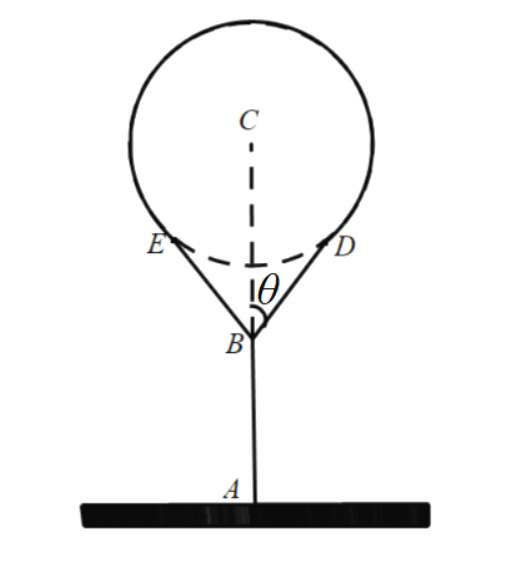
![]() 用
用![]() 表示栈道的总长度
表示栈道的总长度![]() ,并确定
,并确定![]() 的取值范围;
的取值范围;
![]() 求当
求当![]() 为何值时,栈道总长度最短.
为何值时,栈道总长度最短.
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,△PAB是边长为2的等边三角形,底面ABCD为直角梯形,AB∥CD,AB⊥BC,BC=CD=1,PD![]() .
.
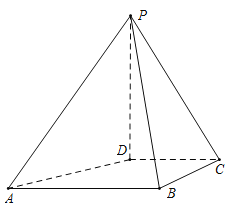
(1)证明:AB⊥PD.
(2)求二面角A﹣PB﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数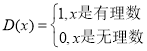 ,被称为狄利克雷函数.以下说法正确的是( ).
,被称为狄利克雷函数.以下说法正确的是( ).
A.![]() 的值域是
的值域是![]()
B.![]() ,都有
,都有![]()
C.存在非零实数![]() ,使得
,使得![]()
D.对任意![]() ,都有
,都有![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .把
.把![]() 沿着
沿着![]() 翻折至
翻折至![]() 的位置,
的位置,![]() 平面
平面![]() ,连结
,连结![]() ,如图2.
,如图2.
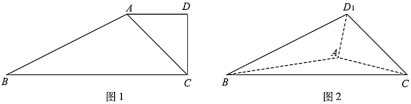
(1)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 的体积最大时,求点
的体积最大时,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的准线与x轴的交点为H,点F为抛物线的焦点,点P在抛物线上且
的准线与x轴的交点为H,点F为抛物线的焦点,点P在抛物线上且![]() ,当k最大时,点P恰好在以H,F为焦点的双曲线上,则k的最大值为_____,此时该双曲线的离心率为_____.
,当k最大时,点P恰好在以H,F为焦点的双曲线上,则k的最大值为_____,此时该双曲线的离心率为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系;曲线C1的普通方程为(x-1)2 +y2 =1,曲线C2的参数方程为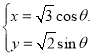 (θ为参数).
(θ为参数).
(Ⅰ)求曲线C1和C2的极坐标方程:
(Ⅱ)设射线θ=![]() (ρ>0)分别与曲线C1和C2相交于A,B两点,求|AB|的值.
(ρ>0)分别与曲线C1和C2相交于A,B两点,求|AB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com