
【题目】某商店为了更好地规划某种商品进货的量,该商店从某一年的销售数据中,随机抽取了![]() 组数据作为研究对象,如下图所示(
组数据作为研究对象,如下图所示(![]() (吨)为该商品进货量,
(吨)为该商品进货量, ![]() (天)为销售天数):
(天)为销售天数):
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅰ)根据上表数据在下列网格中绘制散点图;
(Ⅱ)根据上表提供的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)在该商品进货量![]() (吨)不超过6(吨)的前提下任取两个值,求该商品进货量x(吨)恰有一个值不超过3(吨)的概率.
(吨)不超过6(吨)的前提下任取两个值,求该商品进货量x(吨)恰有一个值不超过3(吨)的概率.
参考公式和数据: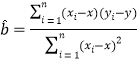 ,
,![]() .
.![]()
【答案】(Ⅰ)见解析(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
(Ⅰ)在平面直角坐标系中画出对应的散点图即可.
(Ⅱ)根据公式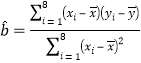 先计算
先计算![]() ,再根据
,再根据![]() 得到
得到![]() .
.
(Ⅲ)通过枚举法可得基本事件的总数,从而得到随机事件“该商品进货量x(吨)恰有一个值不超过3(吨)”所含的基本事件数,由古典概型的概率公式即可得到答案.
(Ⅰ)散点图如图所示:
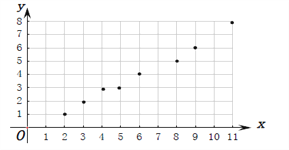
(Ⅱ)依题意,![]() ,
,
![]() .
.
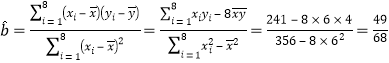 ,
,
故![]() ,回归直线方程为
,回归直线方程为![]() .
.
(Ⅲ)由题意知,在该商品进货量不超过6吨共有5个,设为编码1,2,3,4,5号,任取两个有(1,2)(1,3)(1,4)(1,5)(2,3)(2,4)(2,5)(3,4)(3,5)(4,5)共10种,该商品进货量不超过3吨的有编号1,2号,超过3吨的是编号3,4,5号,该商品进货量恰有一次不超过3吨有(1,3)(1,4)(1,5)(2,3)(2,4)(2,5)共6种,故该商品进货量恰有一次不超过3吨的概率为![]() .
.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源: 题型:
【题目】某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为 ![]() (∠ACB=
(∠ACB= ![]() ),墙AB的长度为6米,(已有两面墙的可利用长度足够大),记∠ABC=θ
),墙AB的长度为6米,(已有两面墙的可利用长度足够大),记∠ABC=θ 
(1)若θ= ![]() ,求△ABC的周长(结果精确到0.01米);
,求△ABC的周长(结果精确到0.01米);
(2)为了使小动物能健康成长,要求所建的三角形露天活动室面积△ABC的面积尽可能大,问当θ为何值时,该活动室面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() ,则关于函数f(x)有以下四个命题( )
,则关于函数f(x)有以下四个命题( )
①x∈R,f(f(x))=1;
②x0 , y0∈R,f(x0+y0)=f(x0)+f(y0);
③函数f(x)是偶函数;
④函数f(x)是周期函数.
其中真命题的个数是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
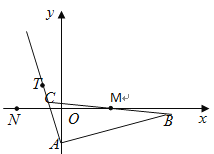
【题目】如图,![]() 的边
的边![]() 边所在直线的方程为
边所在直线的方程为![]()
![]() 满足
满足![]() ,点
,点![]() 在
在![]() 边所在直线上且满足
边所在直线上且满足![]() .
.
(I)求![]() 边所在直线的方程;
边所在直线的方程;
(II)求![]() 的外接圆的方程;
的外接圆的方程;
(III)若点![]() 的坐标为
的坐标为![]() ,其中
,其中![]() 为正整数。试讨论在
为正整数。试讨论在![]() 的外接圆上是否存在点
的外接圆上是否存在点![]() 使得
使得![]() 成立?说明理由.
成立?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(ωx+φ)(ω>0),f'(x)是f(x)的导函数,若f(α)=0,f'(α)>0,且f(x)在区间[α, ![]() +α)上没有最小值,则ω取值范围是( )
+α)上没有最小值,则ω取值范围是( )
A.(0,2)
B.(0,3]
C.(2,3]
D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=30°,AC= ![]() ,D是边AB上一点.
,D是边AB上一点.
(1)求△ABC面积的最大值;
(2)若CD=2,△ACD的面积为2,∠ACD为锐角,求BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足an>1,其前n项和Sn满足6Sn=an2+3an+2
(1)求数列{an}的通项公式及前n项和Sn;
(2)设数列{bn}满足bn= ![]() ,且其前n项和为Tn , 证明:
,且其前n项和为Tn , 证明: ![]() ≤Tn<
≤Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() :
:![]() (
(![]() )和圆
)和圆![]() :
:![]() ,已知圆
,已知圆![]() 将椭圆
将椭圆![]() 的长轴三等分,椭圆
的长轴三等分,椭圆![]() 右焦点到右准线的距离为
右焦点到右准线的距离为![]() ,椭圆
,椭圆![]() 的下顶点为
的下顶点为![]() ,过坐标原点
,过坐标原点![]() 且与坐标轴不重合的任意直线
且与坐标轴不重合的任意直线![]() 与圆
与圆![]() 相交于点
相交于点![]() 、
、![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 、
、![]() 分别与椭圆
分别与椭圆![]() 相交于另一个交点为点
相交于另一个交点为点![]() 、
、![]() .
.
①求证:直线![]() 经过一定点;
经过一定点;
②试问:是否存在以![]() 为圆心,
为圆心,![]() 为半径的圆
为半径的圆![]() ,使得直线
,使得直线![]() 和直线
和直线![]() 都与圆
都与圆![]() 相交?若存在,请求出实数
相交?若存在,请求出实数![]() 的范围;若不存在,请说明理由。
的范围;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com