
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且 ![]() asinA=(
asinA=( ![]() b﹣c)sinB+(
b﹣c)sinB+( ![]() c﹣b)sinC.
c﹣b)sinC.
(1)求角A的大小;
(2)若a= ![]() ,cosB=
,cosB= ![]() ,D为AC的中点,求BD的长.
,D为AC的中点,求BD的长.
【答案】
(1)解:∵ ![]() ,
,
∴由正弦定理可得: ![]() a2=(
a2=( ![]() b﹣c)b+(
b﹣c)b+( ![]() c﹣b)c,即2bc=
c﹣b)c,即2bc= ![]() (b2+c2﹣a2),
(b2+c2﹣a2),
∴由余弦定理可得:cosA= ![]() =
= ![]() ,
,
∵A∈(0,π),
∴A= ![]() .
.
(2)解:∵由cosB= ![]() ,可得sinB=
,可得sinB= ![]() ,
,
再由正弦定理可得 ![]() ,即
,即 ![]() ,
,
∴得b=AC=2.
∵△ABC中,由余弦定理可得BC2=AB2+AC2﹣2ABACcos∠A,
即10=AB2+4﹣2AB2 ![]() ,
,
求得AB=32.
△ABD中,由余弦定理可得BD2=AB2+AD2﹣2ABADcos∠A=18+1﹣6 ![]()
![]() =13,
=13,
∴BD= ![]()
【解析】(I)由已知,利用正弦定理可得 ![]() a2=(
a2=( ![]() b﹣c)b+(
b﹣c)b+( ![]() c﹣b)c,化简可得2bc=
c﹣b)c,化简可得2bc= ![]() (b2+c2﹣a2),再利用余弦定理即可得出cosA,结合A的范围即可得解A的值.(Ⅱ)△ABC中,先由正弦定理求得AC的值,再由余弦定理求得AB的值,△ABD中,由余弦定理求得BD的值.
(b2+c2﹣a2),再利用余弦定理即可得出cosA,结合A的范围即可得解A的值.(Ⅱ)△ABC中,先由正弦定理求得AC的值,再由余弦定理求得AB的值,△ABD中,由余弦定理求得BD的值.


科目:高中数学 来源: 题型:
【题目】一个透明密闭的正方体容器中,恰好盛有该容器一半容积的水,任意转动这个正方体,则水面在容器中的形状可以是:
①三角形;②矩形;③正方形;④正六边形.
其中正确的结论是(把你认为正确的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn=4an﹣3(n∈N*).
(Ⅰ)证明:数列{an}是等比数列;
(Ⅱ)若数列{bn}满足bn+1=an+bn(n∈N*),且b1=2,求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sin2x的图象向左平移 ![]() 个单位,再向上平移1个单位,所得图象的函数解析式是( )
个单位,再向上平移1个单位,所得图象的函数解析式是( )
A.y=cos2x
B.y=2cos2x
C.![]()
D.y=2sin2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设小明订了一份报纸,送报人可能在早上6:30—7:30之间把报纸送到,小明离家的时间在早上7:00—8:00之间,则他在离开家之前能拿到报纸的概率( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1=1,E,F分别是CC1 , BC的中点.
(Ⅰ)求证:B1F⊥平面AEF;
(Ⅱ)求三棱锥E﹣AB1F的体积.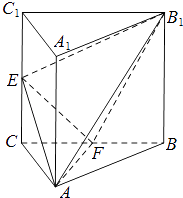
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2﹣3x,则函数g(x)=f(x)﹣x+3的零点的集合为( )
A.{1,3}
B.{﹣3,﹣1,1,3}
C.{2﹣ ![]() ,1,3}
,1,3}
D.{﹣2﹣ ![]() ,1,3}
,1,3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个说法:
①若函数f(x)=asinx+cosx(x∈R)的图象关于直线x= ![]() 对称,则a=
对称,则a= ![]() ;
;
②已知向量 ![]() =(1,2),
=(1,2), ![]() =(﹣2,m),若
=(﹣2,m),若 ![]() 与
与 ![]() 的夹角为钝角,则m<1;
的夹角为钝角,则m<1;
③当 ![]() <α<
<α< ![]() 时,函数f(x)=sinx﹣logax有三个零点;
时,函数f(x)=sinx﹣logax有三个零点;
④函数f(x)=xsinx在[﹣ ![]() ,0]上单调递减,在[0,
,0]上单调递减,在[0, ![]() ]上单调递增.
]上单调递增.
其中正确的是(填上所有正确说法的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com