
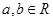 ,若矩阵A=
,若矩阵A=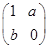 的变换把直线
的变换把直线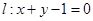 变换为另一直线
变换为另一直线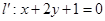 .
.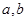 的值;
的值; ;(2)矩阵A的特征值
;(2)矩阵A的特征值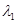 =
=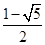 ,
,
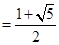 .
.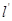 上的点
上的点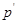 点坐标,列出矩阵变换的表达式,得到等量关系,将得到的点
点坐标,列出矩阵变换的表达式,得到等量关系,将得到的点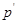 坐标代入直线
坐标代入直线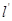 上,得到x与y的关系式,与直线l相对比,得到等量关系,解出a和b;第二问,结合(1)的结论,先得到矩阵A写出特征矩阵,计算出特征多项式
上,得到x与y的关系式,与直线l相对比,得到等量关系,解出a和b;第二问,结合(1)的结论,先得到矩阵A写出特征矩阵,计算出特征多项式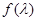 ,通过
,通过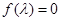 得到矩阵A的特征值.
得到矩阵A的特征值.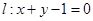 上的任一点
上的任一点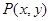 在变换作用下变成了
在变换作用下变成了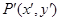 ,
, ,
,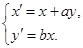 1分
1分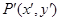 在直线
在直线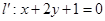 上,
上,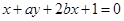 ,
, 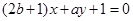 , 2
, 2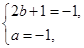
 . 4分
. 4分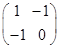 ,
,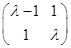 . 5分
. 5分
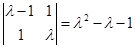 ,
, 0,解得矩阵A的特征值
0,解得矩阵A的特征值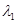 =
=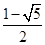 ,
,
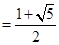 , 7分
, 7分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com