
【题目】已知 ![]() 是函数
是函数 ![]() 的导数,
的导数, ![]() 有
有 ![]() ,
, ![]() ,若
,若 ![]() ,则实数
,则实数 ![]() 的取值范围为 .
的取值范围为 .
【答案】![]()
【解析】构造函数 ![]() ,则
,则 ![]() 可等价转化为
可等价转化为 ![]() ,又因为
,又因为 ![]() ,所以当
,所以当 ![]() 时,
时, ![]() ,函数
,函数 ![]() 单调递减;当
单调递减;当 ![]() 时,
时, ![]() ,函数
,函数 ![]() 单调递增;所以函数
单调递增;所以函数 ![]() 的图像开口向下,且关于直线
的图像开口向下,且关于直线 ![]() 对称,则问题转化为
对称,则问题转化为 ![]() 是否都在一个单调区间内的问题.若
是否都在一个单调区间内的问题.若 ![]() ,则由函数的单调性可知
,则由函数的单调性可知 ![]() ,这与题设
,这与题设 ![]() 矛盾,故
矛盾,故 ![]() ,则
,则 ![]() ,当
,当 ![]() ,则
,则 ![]() ,
, ![]() 的解集是
的解集是 ![]() ;当
;当 ![]() 时,则
时,则 ![]() ,则
,则 ![]() 可化为
可化为 ![]() ,其解集是
,其解集是 ![]() ;若
;若 ![]() ,
, ![]() ,函数
,函数 ![]() 单调递增,则由
单调递增,则由 ![]() 可得
可得 ![]() 不符假设.综上所求实数的取值范围是
不符假设.综上所求实数的取值范围是 ![]() 或
或 ![]() ,即
,即 ![]() .
.
所以答案是:![]() .
.
【考点精析】关于本题考查的利用导数研究函数的单调性,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能得出正确答案.
在这个区间单调递减才能得出正确答案.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】一批产品抽50件测试,其净重介于13克与19克之间,将测试结果按如下方式分成六组:第一组,净重大于等于13克且小于14克;第二组,净重大于等于14克且小于15克;…第六组,净重大于等于18克且小于19克.如图是按上述分组方法得到的频率分布直方图.设净重小于17克的产品数占抽取数的百分比为x,净重大于等于15克且小于17克的产品数为y,则从频率分布直方图中可分析出x和y分别为( )
A.0.9,35
B.0.9,45
C.0.1,35
D.0.1,45
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 为定义域
为定义域![]() 上的单调函数,且存在区间
上的单调函数,且存在区间![]() (其中
(其中![]() ,使得当
,使得当![]() 时,
时,![]() 的取值范围恰为
的取值范围恰为![]() ,则称函数
,则称函数![]() 是
是![]() 上的正函数,区间
上的正函数,区间![]() 叫做函数的等域区间.
叫做函数的等域区间.
(1)已知![]() 是
是![]() 上的正函数,求
上的正函数,求![]() 的等域区间;
的等域区间;
(2)试探求是否存在![]() ,使得函数
,使得函数![]() 是
是![]() 上的正函数?若存在,请求出实数
上的正函数?若存在,请求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是数列
是数列![]() 的前n项和,
的前n项和,![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)对于正整数![]() ,已知
,已知![]() 成等差数列,求正整数
成等差数列,求正整数![]() 的值;
的值;
(3)设数列![]() 前n项和是
前n项和是![]() ,且满足:对任意的正整数n,都有等式
,且满足:对任意的正整数n,都有等式![]() 成立.求满足等式
成立.求满足等式![]() 的所有正整数n.
的所有正整数n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个角形海湾AOB,∠AOB=2θ(常数θ为锐角).拟用长度为l(l为常数)的围网围成一个养殖区,有以下两种方案可供选择:
方案一 如图1,围成扇形养殖区OPQ,其中![]() =l;
=l;
方案二 如图2,围成三角形养殖区OCD,其中CD=l;

(1)求方案一中养殖区的面积S1 ;
(2)求证:方案二中养殖区的最大面积S2=![]() ;
;
(3)为使养殖区的面积最大,应选择何种方案?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的顶点坐标为
的顶点坐标为![]() ,
,![]() ,
,![]() , 点P的横坐标为14,且
, 点P的横坐标为14,且![]() ,点
,点![]() 是边
是边![]() 上一点,且
上一点,且![]() .
.
(1)求实数![]() 的值及点
的值及点![]() 、
、![]() 的坐标;
的坐标;
(2)若![]() 为线段
为线段![]() (含端点)上的一个动点,试求
(含端点)上的一个动点,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(0,+∞)上的函数f(x)满足f′(x)+2f(x)= ![]() ,且f(1)=
,且f(1)= ![]() ,则不等式f(lnx)>f(3)的解集为( )
,则不等式f(lnx)>f(3)的解集为( )
A.(﹣∞,e3)
B.(0,e3)
C.(1,e3)
D.(e3 , +∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方形![]() 的对角线
的对角线![]() 与
与![]() 相交于
相交于![]() 点,将
点,将![]() 沿对角线折起,使得平面
沿对角线折起,使得平面![]() 平面
平面![]() (如图),则下列命题中正确的是( )
(如图),则下列命题中正确的是( )
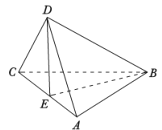
A. 直线![]() 直线
直线![]() ,且直线
,且直线![]() 直线
直线![]()
B. 直线![]() 平面
平面![]() ,且直线
,且直线![]() 平面
平面![]()
C. 平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]()
D. 平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱 ![]() ,侧面
,侧面 ![]() .
.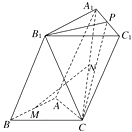
(Ⅰ)若 ![]() 分别是
分别是 ![]() 的中点,求证:
的中点,求证: ![]() ;
;
(Ⅱ)若三棱柱 ![]() 的各棱长均为2,侧棱
的各棱长均为2,侧棱 ![]() 与底面
与底面 ![]() 所成的角为
所成的角为 ![]() ,问在线段
,问在线段 ![]() 上是否存在一点
上是否存在一点 ![]() ,使得平面
,使得平面 ![]() ?若存在,求
?若存在,求 ![]() 与
与 ![]() 的比值,若不存在,说明理由.
的比值,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com