
【题目】设命题P:实数x满足2x2﹣5ax﹣3a2<0,其中a>0,命题q:实数x满足 ![]() .
.
(1)若a=2,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=2,BC= ![]() ,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为( )
,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,焦点在x轴上,离心率为 ![]() ,且经过点M(4,1),直线l:y=x+m交椭圆于不同的两点A,B. (Ⅰ)求椭圆的方程;
,且经过点M(4,1),直线l:y=x+m交椭圆于不同的两点A,B. (Ⅰ)求椭圆的方程;
(Ⅱ)求m的取值范围;
(Ⅲ)若直线l不过点M,求证:直线MA、MB与x轴围成一个等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥ABCD中,BC=DC=AB=AD= ![]() ,BD=2,平面ABD⊥平面BCD,O为BD的中点,P、Q分别为线段AO,BC上的动点,且AP=CQ,求三棱锥PQCO体积的最大值.
,BD=2,平面ABD⊥平面BCD,O为BD的中点,P、Q分别为线段AO,BC上的动点,且AP=CQ,求三棱锥PQCO体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
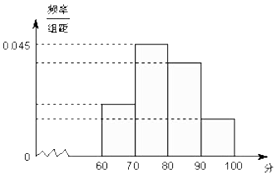
【题目】下面是被严重破坏的频率分布表和频率分布直方图,根据残表和残图,则 p= , q= .
分数段 | 频数 | |
[60,70) | p | |
[70,80) | 90 | |
[80,90) | 60 | |
[90,100] | 20 | q |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四名选手 A、B、C、D 参加射击、抛球、走独木桥三项比赛,每个选手在各项比赛中获得合格、不合格机会相等,比赛结束,评委们会根据选手表现给每位选手评定比赛成绩,根据比赛成绩,对前两名进行奖励.
(1)选手 D 至少获得两个合格的概率;
(2)选手 C、D 只有一人得到奖励的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=3n2+8n,{bn}是等差数列,且an=bn+bn+1 . (Ⅰ)求数列{bn}的通项公式;
(Ⅱ)令cn= ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD,底面ABCD为边长为2对的菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点. 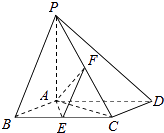
(1)判定AE与PD是否垂直,并说明理由;
(2)若PA=2,求二面角E﹣AF﹣C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com