已知点F( 1,0),⊙F与直线4x+3y+1=0相切,动圆M与⊙F及y轴都相切.
(I )求点M的轨迹C的方程;
(II)过点F任作直线l,交曲线C于A,B两点,由点A,B分别向⊙F各引一条切线,切点 分别为P,Q,记α=∠PAF,β=∠QBF.求证sinα+sinβ是定值.
解:(Ⅰ)⊙F的半径r
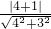
=1,∴⊙F的方程为(x-1)
2+y
2=1,
由题意动圆M与⊙F及y轴都相切,分以下情况:
(1)动圆M与⊙F及y轴都相切,但切点不是原点的情况:
作MH⊥y轴于H,则|MF|-1=|MH|,即|MF|=|MH|+1,
过M作直线x=-1的垂线MN,N为垂足,
则|MF|=|MN|,
∴点M的轨迹是以F为焦点,x=-1为准线的抛物线,
∴点M的轨迹C的方程为y
2=4x(x≠0);
(2)动圆M与⊙F及y轴都相切且仅切于原点的情况:
此时点M的轨迹C的方程为y=0(x≠0,1);
(Ⅱ)对于(Ⅰ)中(1)的情况:
当l不与x轴垂直时,设直线l的方程为y=k(x-1),
由

得k
2x
2-(2k
2+4)x+k
2=0,
设A(x
1,y
1),B(x
2,y
2),
则
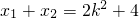
,x
1x
2=1,
∴sinα+sinβ=
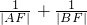
=
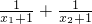
=
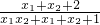
=1.
当l与x轴垂直时,也可得sinα+sinβ=1,
对于(Ⅰ)中(2)的情况不符合题意(即作直线l,交C于一个点或无数个点,而非两个交点).
综上,有sinα+sinβ=1.
分析:(Ⅰ)利用点到直线的距离公式及切线的性质、圆的标准方程即可得到⊙F的方程;动圆M与⊙F及y轴都相切分切点不是原点、切点是原点两种情况分别求出即可:
(Ⅱ)对直线l的斜率分存在和不存在两种情况:把直线的方程与抛物线的方程联立,利用根与系数的关系及抛物线的定义即可得出.
点评:熟练掌握点到直线的距离公式、圆的标准方程及切线的性质、分类讨论的思想方法、直线的方程与抛物线的方程联立并利用根与系数的关系及抛物线的定义是解题的关键.

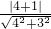 =1,∴⊙F的方程为(x-1)2+y2=1,
=1,∴⊙F的方程为(x-1)2+y2=1, 得k2x2-(2k2+4)x+k2=0,
得k2x2-(2k2+4)x+k2=0,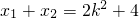 ,x1x2=1,
,x1x2=1,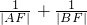 =
=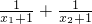 =
=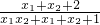 =1.
=1.

 如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,若
如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,若