练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    求经过A(-2，-4)且与直线l:x+3y-26=0相切于点B(8，6)的圆的方程.

    【探究】  根据本题的条件，既可以设圆的一般方程，也可以设圆的标准方程进行求解.

    解法一：设圆的方程为x2+y2+Dx+Ey+F=0，

    则由已知得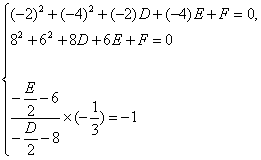

    整理得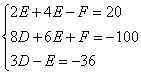，解得D=-11,E=3,F=-30.

    ∴所求圆的方程为x2+y2-11x+3y-30=0.

    解法二：设圆心C(a,b)且圆的方程为(x-a)2+(y-b)2=r2.

    ∵|CA|=|CB|，CB⊥l，

    ∴

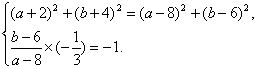
    解得a=,b=，从而r=.

    故所求的方程为.

    【规律总结】 (1)求圆的方程的基本方法：确定圆的方程需要三个独立条件，“选标准，定参数”是解题的基本方法.其中，选标准是根据已知条件选恰当的圆的方程的形式，进而确定其中三个参数.一般来讲，条件涉及到圆上的点多，可选择一般方程，条件涉及到圆心与半径，可选择标准方程.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    9、求经过A（4，2），B（-1，3）两点，且在两坐标轴上的四个截距之和是2的圆的方程为
    x2+y2-2x-12=0
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）已知直线l1：ax+3y+1=0，l2：2x+（a+1）y+1=0
    ①若l1∥l2，求实数a的值；   
    ②若l1⊥l2，求实数a的值．
    （2）已知平面上三个定点A（-1，0），B（3，0），C（1，4）．
    ①求点B到直线AC的距离；
    ②求经过A、B、C三点的圆的方程．

    查看答案和解析>>

    科目：高中数学 来源：学习周报　数学　人教课标高一版(A必修2)　2009－2010学年　第20期　总176期 人教课标高一版 题型：044

    求经过A(2，4)，B(3，3)两点的直线的斜率k和倾斜角α．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求经过A(-2，-4)且与直线l:x+3y-26=0相切于点B(8，6)的圆的方程.

    查看答案和解析>>

    同步练习册答案