【题目】三棱锥P-ABC中，PC
平面ABC，PC=AC=2，AB=BC，D是PB上一点，且CD
平面PAB
(1)求证：AB
平面PCB
(2)求异面直线AP与BC所成角的大小
(3)求二面角C-PA-B 的大小的余弦值
【答案】(1)证明见解析；(2) 
；(3) 
.
【解析】试题分析：（1）
PC
平面ABC，AB
平面ABC，
PCAB，
CD平面PAB，AB平面PAB，CDAB。又
，AB平面PCB
（2）由（1）AB平面PCB ，PC=AC=2， 又AB=BC， 可求得BC=
以B为原点，如图建立空间直角坐标系，
则A（0，，0），B（0，0，0）， C（，0，0） P（，0，2）
=（，-，2），
=（，0，0） 则
=
+0+0=2
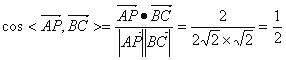
异面直线AP与BC所成的角为
（3）设平面PAB的法向量为m=（x，y，z）
=（0，-，0），=（， 
，2）
则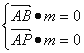
，即，得m=（，0，-1）设平面PAC的法向量为n=（x，y，z）
=（0，0，-2），
=（，-，0），则
得n=（1，1，0）cos<m,n>=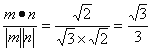
二面角C-PA-B大小的余弦值为
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=lnx，g（x）= 
ax2+bx，a≠0．
（Ⅰ）若b=2，且h（x）=f（x）﹣g（x）存在单调递减区间，求a的取值范围；
（Ⅱ）设函数f（x）的图象C1与函数g（x）图象C2交于点P、Q，过线段PQ的中点作x轴的垂线分别交C1 ， C2于点M、N，证明C1在点M处的切线与C2在点N处的切线不平行．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙两人进行围棋比赛，约定每局胜者得1分，负者得0分，比赛进行到有一人比对方多2分或打满8局时停止.设甲在每局中获胜的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
.
（1）求
的值；
（2）设
表示比赛停止时已比赛的局数，求随机变量的分布列和数学期望
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下面有五个命题：
①函数y=sin4x-cos4x的最小正周期是
；
②终边在y轴上的角的集合是{α|α=
；
③在同一坐标系中，函数y=sinx的图象和函数y=x的图象有三个公共点；
④把函数
；
⑤函数
。
其中真命题的序号是__________（写出所有真命题的编号）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设斜率为2的直线l，过双曲线
的右焦 点，且与双曲线的左、右两支分别相交，则双曲线离心率，e的取值范围是 （ ）
A. e＞
B. e＞
C. 1＜e＜
D. 1＜e＜
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为响应党中央“扶贫攻坚”的号召，某单位指导一贫困村通过种植紫甘薯来提高经济收入.紫甘薯对环境温度要求较高，根据以往的经验，随着温度的升高，其死亡株数成增长的趋势.下表给出了2018年种植的一批试验紫甘薯在不同温度时6组死亡的株数：
温度 | 21 | 23 | 24 | 27 | 29 | 32 |
死亡数 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算：
，
，
，
.
其中
分别为试验数据中的温度和死亡株数，
．
(1)
与
是否有较强的线性相关性? 请计算相关系数
(精确到
)说明.
(2)并求关于的回归方程
(
和
都精确到)；
(3)用(2)中的线性回归模型预测温度为
时该批紫甘薯死亡株数(结果取整数)．
附：对于一组数据
，
，……，
，
①线性相关系数
，通常情况下当
大于0.8时，认为两
个变量有很强的线性相关性．
②其回归直线
的斜率和截距的最小二乘估计分别为：
；
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知椭圆
，过点
，离心率为
，左、右焦点分别为
、
．点
为直线
上且不在
轴上的任意一点，直线
和
与椭圆的交点分别为
、
和
、
，
为坐标原点．
（
）求椭圆的标准方程；
（
）设直线、斜率分别为
、
．
①证明：
；
②问直线
上是否存在一点，使直线
、
、
、
的斜率
、
、
、
满足
？若存在，求出所有满足条件的点的坐标；若不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，矩形ABCD的两条对角线相交于点M(2，0)，AB边所在直线的方程为x－3y－6＝0，点T(－1，1)在AD边所在直线上．求：
(1) AD边所在直线的方程；
(2) DC边所在直线的方程．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
