
定义在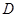 上的函数
上的函数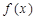 ,如果满足:对任意
,如果满足:对任意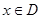 ,存在常数
,存在常数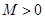 ,都有
,都有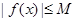 成立,则称
成立,则称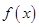 是
是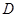 上的有界函数,其中
上的有界函数,其中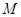 称为函数
称为函数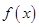 的上界.
的上界.
已知函数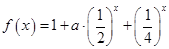 ;
;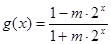 .
.
(1)当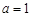 时,求函数
时,求函数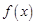 在
在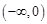 上的值域,并判断函数
上的值域,并判断函数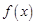 在
在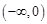 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数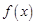 在
在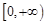 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数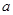 的取值范围;
的取值范围;
(3)若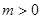 ,函数
,函数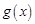 在
在 上的上界是
上的上界是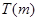 ,求
,求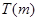 的取值范围.
的取值范围.
(1)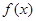 在
在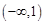 的值域为
的值域为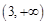 ,故不存在常数
,故不存在常数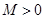 ,使
,使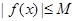 成立
成立
所以函数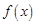 在
在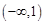 上不是有界函数。
上不是有界函数。
(2)实数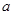 的取值范围为
的取值范围为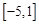 。
。
(3)当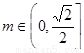 时,
时,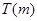 的取值范围是
的取值范围是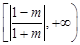 ;
;
当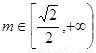 时,
时,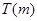 的取值范围是
的取值范围是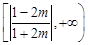
【解析】[解]:(1)当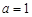 时,
时,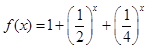
因为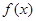 在
在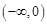 上递减,所以
上递减,所以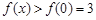 ,即
,即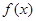 在
在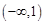 的值域为
的值域为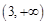
故不存在常数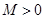 ,使
,使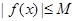 成立
成立
所以函数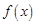 在
在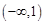 上不是有界函数。 ……………4分(没有判断过程,扣2分)
上不是有界函数。 ……………4分(没有判断过程,扣2分)
(2)由题意知,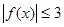 在
在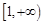 上恒成立。………5分
上恒成立。………5分
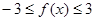 ,
, 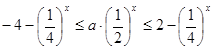
∴ 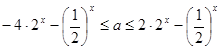 在
在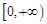 上恒成立………6分
上恒成立………6分
∴ 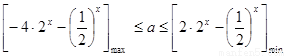 ………7分
………7分
设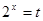 ,
,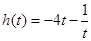 ,
,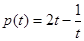 ,由
,由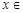
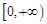 得 t≥1,
得 t≥1,
设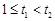 ,
,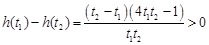
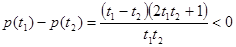
所以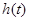 在
在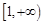 上递减,
上递减,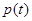 在
在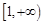 上递增,………9分(单调性不证,不扣分)
上递增,………9分(单调性不证,不扣分)
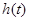 在
在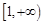 上的最大值为
上的最大值为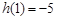 ,
, 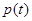 在
在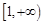 上的最小值为
上的最小值为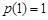
所以实数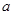 的取值范围为
的取值范围为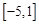 。…………………………………11分
。…………………………………11分
(3)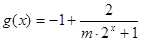 ,∵ m>0 ,
,∵ m>0 ,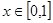 ∴
∴ 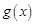 在
在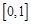 上递减,…12分
上递减,…12分
∴ 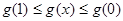 即
即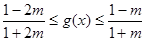 ………13分
………13分
①当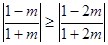 ,即
,即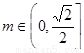 时,
时, , ………14分
, ………14分
此时 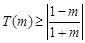 ,………16分②当
,………16分②当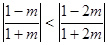 ,即
,即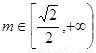 时,
时,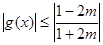 ,
,
此时  , ---------17分
, ---------17分
综上所述,当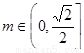 时,
时,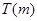 的取值范围是
的取值范围是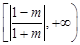 ;
;
当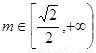 时,
时,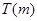 的取值范围是
的取值范围是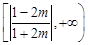 ………18分
………18分


科目:高中数学 来源:2015届四川成都七中实验学校高一3月月考数学试卷(解析版) 题型:选择题
定义在 上的函数
上的函数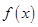 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 ,
, 仍是等比数列,则称
仍是等比数列,则称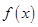 为“保等比数列函数”. 现有定义在
为“保等比数列函数”. 现有定义在 上的如下函数:
上的如下函数:
①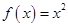 ②
② ③
③ ④
④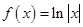
则其中是“保等比数列函数”的 的序号为( )
的序号为( )
A.①② B.③④ C.①③ D.②④
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省东莞市高三第三次月考理科数学试卷(解析版) 题型:选择题
定义在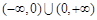 上的函数
上的函数 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 ,
, 仍是等比数列,则称
仍是等比数列,则称 为“保等比数列函数”. 现有定义在
为“保等比数列函数”. 现有定义在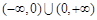 上的如下函数:
上的如下函数:
① ; ②
; ② ; ③
; ③ ; ④
; ④ .
.
则其中是“保等比数列函数”的 的序号为( )
的序号为( )
A.① ② B.③ ④ C.① ③ D.② ④
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试理科数学(湖北卷解析版) 题型:选择题
定义在 上的函数
上的函数 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列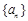 ,
,  仍是等比数列,则称
仍是等比数列,则称 为“保等比数列函数”. 现有定义在
为“保等比数列函数”. 现有定义在 上的如下函数:①
上的如下函数:① ; ②
; ② ; ③
; ③ ; ④
; ④ .则其中是“保等比数列函数”的
.则其中是“保等比数列函数”的 的序号为
的序号为
A、① ② B、③ ④ C、① ③ D、② ④
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试文科数学(湖北卷解析版) 题型:选择题
定义在 上的函数
上的函数 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 仍是等比数列,则称
仍是等比数列,则称 为“保等比数列函数”。现有定义在
为“保等比数列函数”。现有定义在 上的如下函数:①
上的如下函数:① ;②
;② ;③
;③ ;④
;④ 。则其中是“保等比数列函数”的
。则其中是“保等比数列函数”的 的序号为
的序号为
A、①② B、③④ C、①③ D、②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com