练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设函数，其中、.

    （1）若曲线在点处的切线方程为，求，的值；

    （2）当时，恒成立，求满足条件的最小整数的值.

    【答案】见解析

    【解析】（1）由，得.

    由题意得，解得 ，.…………………3分

    （2）由，得.

    设，则.

    因为，所以，则在上单调递增.

    又，，

    所以存在，使得. …………………6分

    于是在上单调递减，在上单调递增.

    ∴，

    则.

    又，即，所以.…………………9分

    于是，即.

    由得，.

    从而，恒成立.

    令，，则.

    又设，则.

    所以在上单调递增，且.

    则，即在上单调递增.

    于是.

    所以.

    故满足条件的最小整数的值为. …………………12分

    【命题意图】本题主要考查导数的综合应用，涉及导数的几何意义、利用导数判断函数的单调性等，意在考查学生的运算求解能力、推理论证能力以及分析问题、解决问题的能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥P－ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA＝AB＝BC＝2，D为线段AC的中点，E为线段PC上一点.

    (1)求证：PA⊥BD；

    (2)求证：平面BDE⊥平面PAC；

    (3)当PA∥平面BDE时，求三棱锥E－BCD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数=().

    （Ⅰ）当=-3时，求的极值；

    （Ⅱ）当>1时，＞0,求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-5：不等式选讲

    已知函数（）.

    （1）若，求不等式的解集；

    （2）若对于任意的，，都有恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面四边形ABCD中，DA⊥AB，

    DE＝1，EC＝，EA＝2，

    ∠ADC＝，∠BEC＝.

    (Ⅰ)求sin∠CED的值；

    (Ⅱ)求BE的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列的前项和，且是2与的等差中项.

    （1）求数列的通项公式；

    （2）若，求数列的前项和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥E﹣ABCD中，底面ABCD是矩形，AB=1，AE⊥平面CDE， ，F为线段DE上的一点．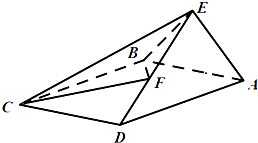

    （1）求证：平面AED⊥平面ABCD；
    （2）若二面角E﹣BC﹣F与二面角F﹣BC﹣D的大小相等，求DF的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数的部分图像如图所示，将的图象向右平移个单位长度后得到函数的图象.

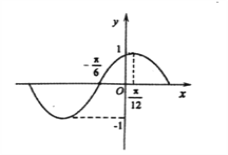
    （1）求函数的解析式；

    （2）在中，角A,B,C满足，且其外接圆的半径R=2，求的面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解某校学生的视力情况，现采用随机抽样的方法从该校的两班中各抽取名学生进行视力检测，检测的数据如下:

    班名学生的视力检测结果：

    班名学生的视力检测结果：

    （Ⅰ）分别计算两组数据的平均数，从计算结果看，哪个班的学生的视力较好？并计算班的名学生视力的方差；

    （Ⅱ）现从班的上述名学生中随机选取名，求这名学生中至少有名学生的视力低于的概率.

    查看答案和解析>>

    同步练习册答案