
【题目】已知数列 ![]() 的各项均为正整数,对于任意n∈N* , 都有
的各项均为正整数,对于任意n∈N* , 都有 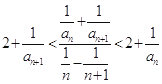 成立,且
成立,且 ![]() .
.
(1)求 ![]() ,
, ![]() 的值;
的值;
(2)猜想数列 ![]() 的通项公式,并给出证明.
的通项公式,并给出证明.
【答案】
(1)
解:因为 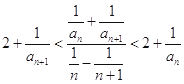 ,
, ![]()
当 ![]() 时,由
时,由 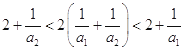 ,即有
,即有 ![]() ,
,
解得 ![]() .因为
.因为 ![]() 为正整数,故
为正整数,故 ![]() .
.
当 ![]() 时,由
时,由 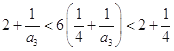 ,
,
解得 ![]() ,所以
,所以 ![]() .
.
(2)
解:由 ![]() ,
, ![]() ,
, ![]() ,猜想:
,猜想: ![]()
下面用数学归纳法证明.
①当 ![]() ,
, ![]() ,
, ![]() 时,由(1)知
时,由(1)知 ![]() 均成立.
均成立.
②假设 ![]() 成立,则
成立,则 ![]() ,
,
由条件得 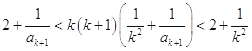 ,
,
所以 ![]() ,
,
所以 ![]()
因为 ![]() ,
, ![]() ,
, ![]() ,
,
又 ![]() ,所以
,所以 ![]() .
.
即 ![]() 时,
时, ![]() 也成立.
也成立.
由①,②知,对任意 ![]() ,
, ![]() .
.
【解析】本题主要考查了数学归纳法证明不等式,解决问题的关键是根据(1)先列出 ![]() 所满足条件
所满足条件 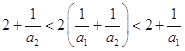 ,化简得
,化简得 ![]() ,再根据数列
,再根据数列 ![]() 的各项均为正整数这一限制条件求出
的各项均为正整数这一限制条件求出 ![]() ,同理可得
,同理可得 ![]() (2)猜想:
(2)猜想: ![]() ,用数学归纳法证明的关键由k成立推出k+1成立,其推导思路同(1):由条件得
,用数学归纳法证明的关键由k成立推出k+1成立,其推导思路同(1):由条件得 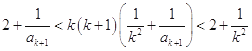 ,所以
,所以 ![]() ,所以
,所以 ![]() 因为
因为 ![]() ,
, ![]() ,
, ![]() ,所以
,所以 ![]()


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+m21﹣x .
(1)若函数f(x)为奇函数,求实数m的值;
(2)若函数f(x)在区间(1,+∞)上是单调递增函数,求实数m的取值范围;
(3)是否存在实数a,使得函数f(x)的图象关于点A(a,0)对称,若存在,求实数a的值,若不存在,请说明理由.
注:点M(x1 , y1),N(x2 , y2)的中点坐标为( ![]() ,
, ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2+(b﹣8)x﹣a﹣ab的两个零点分别是﹣3和2.
(Ⅰ)求f(x);
(Ⅱ)当函数f(x)的定义域是[0,1]时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班20名同学某次数学测试的成绩可绘制成如图茎叶图.由于其中部分数据缺失,故打算根据茎叶图中的数据估计全班同学的平均成绩.


(1)完成频率分布直方图;
(2)根据(1)中的频率分布直方图估计全班同学的平均成绩![]() (同一组中的数据用改组区间的中点值作代表);
(同一组中的数据用改组区间的中点值作代表);
(3)根据茎叶图计算出的全班的平均成绩为![]() ,并假设
,并假设![]() ,且
,且![]() 取得每一个可能值的机会相等,在(2)的条件下,求概率
取得每一个可能值的机会相等,在(2)的条件下,求概率![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校举行的一次数学竞赛中,全体参赛学生的竞赛成绩X近似服从正态分布N(70,100).已知成绩在90分以上(含90分)的学生有16名.
(1)试问此次参赛的学生总数约为多少人?
(2)若该校计划奖励竞赛成绩在80分以上(含80分)的学生,试问此次竞赛获奖励的学生约为多少人?
附:P(|X-μ|<σ)=0.683,P(|X-μ|<2σ)=0.954,P(|X-μ|<3σ)=0.997
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com