
【题目】某鲜花店每天制作![]() 、
、![]() 两种鲜花共
两种鲜花共![]() 束,每束鲜花的成本为
束,每束鲜花的成本为![]() 元,售价
元,售价![]() 元,如果当天卖不完,剩下的鲜花作废品处理.该鲜花店发现这两种鲜花每天都有剩余,为此整理了过往100天这两种鲜花的日销量(单位:束),得到如下统计数据:
元,如果当天卖不完,剩下的鲜花作废品处理.该鲜花店发现这两种鲜花每天都有剩余,为此整理了过往100天这两种鲜花的日销量(单位:束),得到如下统计数据:
| 48 | 49 | 50 | 51 |
天数 | 25 | 35 | 20 | 20 |
| 48 | 49 | 50 | 51 |
天数 | 40 | 35 | 15 | 10 |
以这100天记录的各销量的频率作为各销量的概率,假设这两种鲜花的日销量相互独立.
(1)记该店这两种鲜花每日的总销量为![]() 束,求
束,求![]() 的分布列.
的分布列.
(2)鲜花店为了减少浪费,提升利润,决定调查每天制作鲜花的量![]() 束.以销售这两种鲜花的日总利润的期望值为决策依据,在每天所制鲜花能全部卖完与
束.以销售这两种鲜花的日总利润的期望值为决策依据,在每天所制鲜花能全部卖完与![]() 之中选其一,应选哪个?
之中选其一,应选哪个?
【答案】(1)详见解析;(2)应选![]() .
.
【解析】
(1)由题意得到X的可能取值,分别求出相应的概率,由此能求出X的分布列.
(2)由(1)知在每天所制鲜花能全部卖完时,n=96,此时销售的日总利润的期望值为96a.再求出当n=99时,销售的日总利润的期望值,比较可以得到应选n=99.
(1)![]() 所有可能的取值为96,97,98,99,100,101,102,
所有可能的取值为96,97,98,99,100,101,102,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
所以![]() 的分布列为
的分布列为
| 96 | 97 | 98 | 99 | 100 | 101 | 102 |
| 0.1 | 0.2275 | 0.24 | 0.2275 | 0.135 | 0.05 | 0.02 |
(2)记销售两种鲜花的日总利润为![]() .
.
当每天所制鲜花能全部卖完时,![]() ,
,
由于卖出1束利润为![]() 元,作废品处理1束亏
元,作废品处理1束亏![]() 元.
元.
所以![]() 时,
时,![]()
![]()
![]() .
.
所以应选![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知半圆![]() :
:![]() ,
,![]() 、
、![]() 分别为半圆
分别为半圆![]() 与
与![]() 轴的左、右交点,直线
轴的左、右交点,直线![]() 过点
过点![]() 且与
且与![]() 轴垂直,点
轴垂直,点![]() 在直线
在直线![]() 上,纵坐标为
上,纵坐标为![]() ,若在半圆
,若在半圆![]() 上存在点
上存在点![]() 使
使![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=2,AB//DC,AB=2CD,∠BCD=90°.
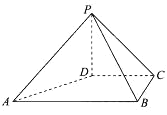
(1)求证:AD⊥PB;
(2)求点C到平面PAB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】七巧板是古代中国劳动人民发明的一种中国传统智力玩具,它由五块等腰直角三角形,一块正方形和一块平行四边形共七块板组成.清陆以湉《冷庐杂识》卷一中写道:近又有七巧图,其式五,其数七,其变化之式多至千余.体物肖形,随手变幻,盖游戏之具,足以排闷破寂,故世俗皆喜为之.如图是一个用七巧板拼成的正方形,若在此正方形中任取一点,则此点取自阴影部分的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年7月18日15时,超强台风“威马逊”登陆海南省.据统计,本次台风造成全省直接经济损失119.52亿元,适逢暑假,小明调查住在自己小区的50户居民由于台风造成的经济损失,作出如下频率分布直方图:
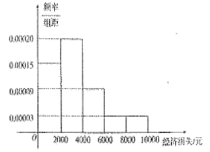
| 经济损失4000元以下 | 经济损失4000元以上 | 合计 |
捐款超过500元 | 30 | ||
捐款低于500元 | 6 | ||
合计 |
(1)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如上表,在表格空白处填写正确数字,并说明是否有![]() 以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
(2)台风造成了小区多户居民门窗损坏,若小区所有居民的门窗均由李师傅和张师傅两人进行维修,李师傅每天早上在7:00到8:00之间的任意时刻来到小区,张师傅每天早上在7:30到8:30分之间的任意时刻来到小区,求连续3天内,李师傅比张师傅早到小区的天数的分布列和数学期望.
附:临界值表
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
参考公式:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为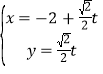 (t为参数).直线
(t为参数).直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:只要
满足:只要![]() ,必有
,必有![]() ,则称
,则称![]() 具有性质
具有性质![]() .
.
(1)若![]() 具有性质
具有性质![]() ,且
,且![]() ,
, ![]() ,求
,求![]() ;
;
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列, ![]() ,
, ![]() ,
, ![]() 判断
判断![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(3)设![]() 是无穷数列,已知
是无穷数列,已知![]() .求证:“对任意
.求证:“对任意![]() 都具有性质
都具有性质![]() ”的充要条件为“
”的充要条件为“![]() 是常数列”.
是常数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心为
的圆心为![]() ,
,![]() 为圆上任意一点,
为圆上任意一点,![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)记点![]() 的轨迹为曲线
的轨迹为曲线![]() ,点
,点![]() ,
,![]() .若点
.若点![]() 为直线
为直线![]() 上一动点,且
上一动点,且![]() 不在
不在![]() 轴上,直线
轴上,直线![]() 、
、![]() 分别交曲线
分别交曲线![]() 于
于![]() 、
、![]() 两点,求四边形
两点,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com