
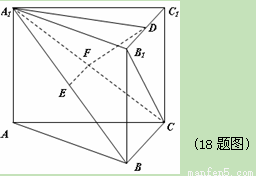
直三棱柱 中,
中,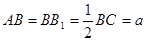 ,
, ,
, 、
、 分别为
分别为 、
、 的中点.
的中点.

(Ⅰ)求证: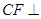 平面
平面 ;
;
(Ⅱ)求四面体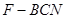 的体积.
的体积.
(Ⅰ)先证AB⊥平面BB1C1C.又N、F分别为A1 C1、B1 C1的中点,证出NF⊥平面BB1C1C. NF⊥FC .
证得FC⊥平面NFB.
(Ⅱ)
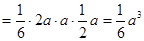 .
.
【解析】
试题分析:(Ⅰ)直三棱柱ABC-A1B1C1中,
B1B⊥AB, BC⊥AB,又B1B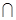 BC=B,
BC=B,
∴AB⊥平面BB1C1C.
又N、F分别为A1 C1、B1 C1的中点
∴AB∥A1B1∥NF.
∴NF⊥平面BB1C1C.
因为FC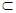 平面BB1C1C.所以NF⊥FC .
平面BB1C1C.所以NF⊥FC .
取BC中点G,有BG=GF=GC.∴BF⊥FC ,又 NF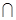 FB=F,
FB=F,
∴FC⊥平面NFB. 7分
(Ⅱ)由(Ⅰ)知, 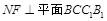 ,
,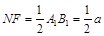 ,
,
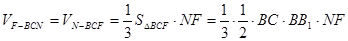
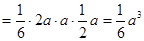 .
14分
.
14分
考点:本题主要考查立体几何中的平行关系、垂直关系,体积计算。
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,若利用向量则可简化证明过程。(2)体积计算中,运用了“等积法”。


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源:2012-2013学年广东惠州高二上学期期中考试文科数学试卷(解析版) 题型:解答题
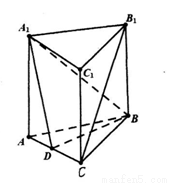
(本小题满分14分) 如图,在直三棱柱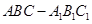 中,
中,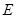 、
、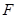 分别是
分别是 、
、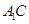 的中点,点
的中点,点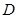 在
在 上,
上,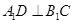 。
。
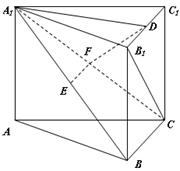
求证:(1)EF∥平面ABC;
(2)平面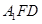
 平面
平面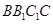
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省陆丰市高二第三次月考理科数学试卷(解析版) 题型:解答题
(本题满分14分)
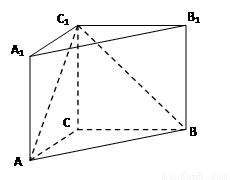
如图, 在直三棱柱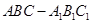 中,
中,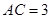 ,
,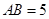 ,
, .
.
(1)求证: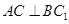 ;
;
(2)问:是否在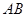 线段上存在一点
线段上存在一点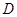 ,使得
,使得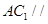 平面
平面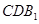 ?
?
若存在,请证明;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年甘肃省河西五市高三第二次联合考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
在直三棱柱中,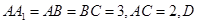 是
是 中点.
中点.
(1)求证: //平面
//平面 ;
;
(2)求点 到平面
到平面 的距离;
的距离;
(3)求二面角 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市嘉定区高三年级第一次质量调研理科数学 题型:解答题
(本题满分12分)本题共有2个小题,第1小题满分5分,第2小题满分7分.
如图,在直三棱柱 中,
中,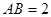 ,
, ,
, .
.
(1)求三棱柱 的表面积
的表面积 ;
;
(2)求异面直线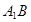 与
与 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).

查看答案和解析>>
科目:高中数学 来源:黑龙江省10-11学年高一下学期期末考试数学(理) 题型:解答题
(本小题满分12分)如图,在直三棱柱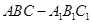 中,
中,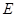 、
、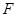 分别是
分别是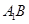 、
、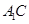 的中 点,点
的中 点,点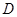 在
在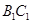 上,
上,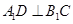 。
。
求证:(1)EF∥平面ABC;
(2)平面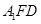
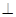 平面
平面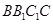 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com