
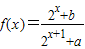 是R上奇函数
是R上奇函数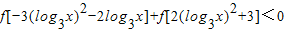 .
.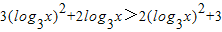 ,解得 log3x 的范围,再解对数不等式即可求得原不等式的解集.
,解得 log3x 的范围,再解对数不等式即可求得原不等式的解集. 是R上奇函数,故有f(0)=0,解得b=-1.
是R上奇函数,故有f(0)=0,解得b=-1. =-
=-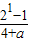 ,解得 a=2.
,解得 a=2.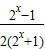 ,经过检验,此函数为奇函数.
,经过检验,此函数为奇函数. -
- ,故函数在R上是单调增函数,故不等式等价于
,故函数在R上是单调增函数,故不等式等价于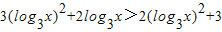 ,
, +2log3x-3>0,
+2log3x-3>0,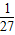 ,或 x>3,
,或 x>3,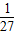 ,或 x>3 }.
,或 x>3 }.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com