
“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度 (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度 (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当 不超过4(尾/立方米)时,
不超过4(尾/立方米)时, 的值为
的值为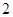 (千克/年);当
(千克/年);当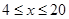 时,
时, 是
是 的一次函数;当
的一次函数;当 达到
达到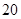 (尾/立方米)时,因缺氧等原因,
(尾/立方米)时,因缺氧等原因, 的值为
的值为 (千克/年).
(千克/年).
(1)当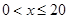 时,求函数
时,求函数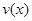 的表达式;
的表达式;
(2)当养殖密度 为多大时,鱼的年生长量(单位:千克/立方米)
为多大时,鱼的年生长量(单位:千克/立方米)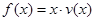 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.
科目:高中数学 来源: 题型:解答题
为了降低能源损耗,某城市对新建住宅的屋顶和外墙都要求建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度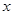 (单位:cm)满足关系:
(单位:cm)满足关系: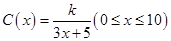 ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设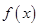 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求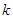 的值及
的值及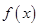 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用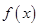 达到最小,并求最小值.
达到最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
随着机构改革工作的深入进行,各单位要减员增效。有一家公司现有职员 人,(
人,( ,且
,且 为偶数),每人每年可创利
为偶数),每人每年可创利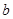 万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利
万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利 万元,但公司需支付下岗职员每人每年
万元,但公司需支付下岗职员每人每年 万元的生活费,并且该公司正常运转所需人数不得小于现有员工的
万元的生活费,并且该公司正常运转所需人数不得小于现有员工的 ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设 是定义在
是定义在 的可导函数,且不恒为0,记
的可导函数,且不恒为0,记 .若对定义域内的每一个
.若对定义域内的每一个 ,总有
,总有 ,则称
,则称 为“
为“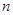 阶负函数 ”;若对定义域内的每一个
阶负函数 ”;若对定义域内的每一个 ,总有
,总有 ,则称
,则称 为“
为“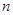 阶不减函数”(
阶不减函数”( 为函数
为函数 的导函数).
的导函数).
(1)若 既是“1阶负函数”,又是“1阶不减函数”,求实数
既是“1阶负函数”,又是“1阶不减函数”,求实数 的取值范围;
的取值范围;
(2)对任给的“2阶不减函数” ,如果存在常数
,如果存在常数 ,使得
,使得 恒成立,试判断
恒成立,试判断 是否为“2阶负函数”?并说明理由.
是否为“2阶负函数”?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数f(x)满足条件f(0)=1和f(x+1)-f(x)=2x.
(1)求f(x);
(2)求f(x)在区间[-1,1]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
进货原价为80元的商品400个,按90元一个售出时,可全部卖出.已知这种商品每个涨价一元,其销售数就减少20个,问售价应为多少时所获得利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com