
【题目】数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() 是
是![]() 和
和![]() 的等差中项,等差数列
的等差中项,等差数列![]() 满足
满足![]() ,
,![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ,
,![]() ;(2)证明过程详见解析.
;(2)证明过程详见解析.
【解析】
试题分析:本题主要考查等差数列与等比数列的概念、通项公式、前![]() 项和公式、数列求和等基础知识,考查运算能力、推理论证能力.第一问,先利用
项和公式、数列求和等基础知识,考查运算能力、推理论证能力.第一问,先利用![]() 是
是![]() 和
和![]() 的等差中项,得到
的等差中项,得到![]() ,由
,由![]() 求
求![]() ,注意
,注意![]() 的情况,不要漏掉,会得到
的情况,不要漏掉,会得到![]() 为等比数列,利用等比数列的通项公式,求和公式直接写出
为等比数列,利用等比数列的通项公式,求和公式直接写出![]() 和
和![]() ,再利用已知求出
,再利用已知求出![]() ,写出等差数列的通项公式;第二问,先化简
,写出等差数列的通项公式;第二问,先化简![]() 表达式,利用裂项相消法求和求
表达式,利用裂项相消法求和求![]() ,利用放缩法比较
,利用放缩法比较![]() 与
与![]() 的大小,作差法判断数列的单调性,因为数列
的大小,作差法判断数列的单调性,因为数列![]() 为递增数列,所以最小值为
为递增数列,所以最小值为![]() ,即
,即![]() ,所以
,所以![]() .
.
试题解析:(1)∵![]() 是
是![]() 和
和![]() 的等差中项,∴
的等差中项,∴![]()
当![]() 时,
时,![]() ,∴
,∴![]()
当![]() 时,
时,![]() ,
,
∴![]() ,即
,即 ![]() 3分
3分
∴数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列,
为公比的等比数列,
∴![]() ,
,![]() 5分
5分
设![]() 的公差为
的公差为![]() ,
,![]() ,
,![]() ,∴
,∴![]()
∴![]() 6分
6分
(2)![]() 7分
7分
∴![]() 9分
9分
∵![]() ,∴
,∴![]() 10分
10分
![]()
∴数列![]() 是一个递增数列 ∴
是一个递增数列 ∴![]() .
.
综上所述,![]() . 12分
. 12分


科目:高中数学 来源: 题型:
【题目】若函数y=f(x)同时满足:(ⅰ)对于定义域内的任意x,恒有f(x)+f(﹣x)=0;(ⅱ)对于定义域内的任意x1 , x2 , 当x1≠x2时,恒有![]() , 则称函数f(x)为“二维函数”.现给出下列四个函数:
, 则称函数f(x)为“二维函数”.现给出下列四个函数:
①f(x)=![]()
②f(x)=﹣x3+x
③![]()
④![]()
其中能被称为“二维函数”的有 (写出所有满足条件的函数的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取40名中学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段: ![]() ,
, ![]() ,…,
,…, ![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
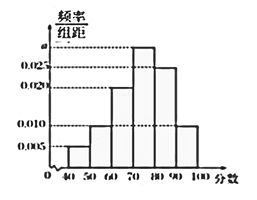
(1)求图中实数![]() 的值;
的值;
(2)若该校高一年级共有640人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在![]() 与
与![]() 两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题:
①“若![]() , 则
, 则![]() 互为相反数”的逆命题;
互为相反数”的逆命题;
②“若两个三角形全等,则两个三角形的面积相等”的否命题;
③“若![]() ,则
,则![]() 有实根”的逆否命题;
有实根”的逆否命题;
④“若![]() 不是等边三角形,则
不是等边三角形,则![]() 的三个内角相等”逆命题;
的三个内角相等”逆命题;
其中真命题为( ).
A. ①② B. ②③ C. ①③ D. ③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左焦点
的左焦点![]() ,若椭圆上存在一点
,若椭圆上存在一点![]() ,满足以椭圆短轴为直径的圆与线段
,满足以椭圆短轴为直径的圆与线段![]() 相切于线段
相切于线段![]() 的中点
的中点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过坐标原点![]() 的直线交椭圆
的直线交椭圆![]() :
: ![]() 于
于![]() 、
、![]() 两点,其中点
两点,其中点![]() 在第一象限,过
在第一象限,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连结
,连结![]() 并延长交椭圆
并延长交椭圆![]() 于
于![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() 的定义域为A,集合B={x|(x﹣m﹣3)(x﹣m+3)≤0}.
的定义域为A,集合B={x|(x﹣m﹣3)(x﹣m+3)≤0}.
(1)求A和f(x)的值域C;
(2)若A∩B=[2,3],求实数m的值;
(3)若CRB,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com