练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

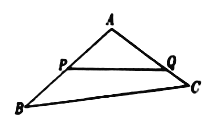
    【题目】如图，某生态园将一块三角形地的一角开辟为水果园，已知角为， 的长度均大于200米，现在边界处建围墙，在处围竹篱笆.

    （1）若围墙、总长度为200米，如何可使得三角形地块面积最大？

    （2）已知竹篱笆长为米， 段围墙高1米， 段围墙高2米，造价均为每平方米100元，若，求围墙总造价的取值范围.

    【答案】（1） (米)， (米2)；（2）.

    【解析】试题分析：

    (1)设 ，利用题意列出面积的表达式，最后利用均值不等式求解最值即可，注意讨论等号成立的条件和实际问题的定义域；

    (2)利用题意结合正弦定理求得围墙造价的函数解析式，利用三角形的性质求得 的范围即可求得造价的取值范围.

    试题解析：

    设 (米)，则,所以 (米2)

    当且仅当时，取等号。即 (米)， (米2)

    (2)由正弦定理， 得

    故围墙总造价

    因为， 所以，

    所以围墙总造价的取值范围为 (元)

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数（， ）.

    （1）当时，讨论函数的单调区间；

    （2）当时，若对任意恒成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆经过点， ，并且直线平分圆.

    （1）求圆的方程；

    （2）若直线与圆交于两点，是否存在直线，使得（为坐标原点），若存在，求出的值；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2﹣lnx．

    （1）求曲线f（x）在点（1，f（1））处的切线方程；

    （2）求函数f（x）的单调递减区间：

    （3）设函数g（x）=f（x）﹣x2+ax，a＞0，若x∈（O，e]时，g（x）的最小值是3，求实数a的值．（e为自然对数的底数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}是公差为2的等差数列，且a1 ， a4 ， a13成等比数列，数列{ }是首项为1，公比为3的等比数列．
    （1）求数列{an}、{bn}的通项公式；
    （2）设数列{an+bn}的前n项和Rn ， 若不等式 ≤λ3n+n+3对n∈N*恒成立，求λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】是等边三角形，边长为4， 边的中点为，椭圆以， 为左、右两焦点，且经过、两点。

    （1）求该椭圆的标准方程；

    （2）过点且轴不垂直的直线交椭圆于， 两点，求证：直线与的交点在一条定直线上.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知曲线的极坐标方程是，以极点为原点，极轴为轴的正半轴建立平面直角坐标系，直线的参数方程为（为参数）.

    （Ⅰ）写出直线的普通方程与曲线的直角坐标方程；

    （Ⅱ）设曲线经过伸缩变换得到曲线，若点，直线与交与， ，求， .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （Ⅰ）讨论的单调性；

    （Ⅱ）当时，讨论的零点个数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C：x2＋y2＋2x－4y＋3＝0．

    (1)若圆C的切线在x轴和y轴上的截距相等，求此切线的方程．

    (2)从圆C外一点P(x1，y1)向该圆引一条切线，切点为M，O为坐标原点，且有|PM|＝|PO|，求使得|PM|取得最小值的点P的坐标．

    查看答案和解析>>

    同步练习册答案