
【题目】数列{![]() n}中
n}中![]() 1=3,已知点(
1=3,已知点(![]() n,
n,![]() n+1)在直线y=x+2上,
n+1)在直线y=x+2上,
(1)求数列{![]() n}的通项公式;
n}的通项公式;
(2)若bn=![]() n3n,求数列{bn}的前n项和Tn.
n3n,求数列{bn}的前n项和Tn.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)把点(![]() n,
n,![]() n+1)代入直线y=x+2中可知数列{
n+1)代入直线y=x+2中可知数列{![]() n}是以3为首项,以2为公差的等差数,进而利用等差数列的通项公式求得答案.
n}是以3为首项,以2为公差的等差数,进而利用等差数列的通项公式求得答案.
(2)把(1)中求得![]() n代入bn=
n代入bn=![]() n3n,利用错位相减法求得数列{bn}的前n项和Tn.
n3n,利用错位相减法求得数列{bn}的前n项和Tn.
(1)∵点(![]() n,
n,![]() n+1)在直线y=x+2上.∴数列{
n+1)在直线y=x+2上.∴数列{![]() n}是以3为首项,以2为公差的等差数列,
n}是以3为首项,以2为公差的等差数列,
∴![]() n=3+2(n﹣1)=2n+1.
n=3+2(n﹣1)=2n+1.
(2)∵bn=![]() n3n,∴bn=(2n+1)3n
n3n,∴bn=(2n+1)3n
∴Tn=3×3+5×32+7×33+…+(2n﹣1)3n﹣1+(2n+1)3n①
∴3Tn=3×32+5×33+…+(2n﹣1)3n+(2n+1)3n+1②
由①﹣②得﹣2Tn=3×3+2(32+33+...+3n)﹣(2n+1)3n+1
=![]() =﹣2n3n+1
=﹣2n3n+1
∴Tn=n3n+1.


科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某公园内有两条道路![]() ,
,![]() ,现计划在
,现计划在![]() 上选择一点
上选择一点![]() ,新建道路
,新建道路![]() ,并把
,并把![]() 所在的区域改造成绿化区域.已知
所在的区域改造成绿化区域.已知![]() ,
,![]()
![]() .
.
(1)若绿化区域![]() 的面积为1
的面积为1![]() ,求道路
,求道路![]() 的长度;
的长度;
(2)若绿化区域![]() 改造成本为10万元/
改造成本为10万元/![]() ,新建道路
,新建道路![]() 成本为10万元/
成本为10万元/![]() .设
.设![]() (
(![]() ),当
),当![]() 为何值时,该计划所需总费用最小?
为何值时,该计划所需总费用最小?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是由容量为100的样本得到的频率分布直方图.其中前4组的频率成等比数列,后6组的频数成等差数列,设最大频率为a,在![]() 到
到![]() 之间的数据个数为b,则a,b的值分别为( )
之间的数据个数为b,则a,b的值分别为( )
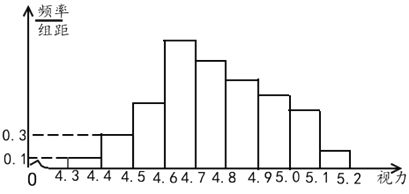
A.![]() ,78
,78
B.![]() ,83
,83
C.![]() ,78
,78
D.![]() ,83
,83
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在平行于
在平行于![]() 轴的直线
轴的直线![]() 上,且
上,且![]() 与
与![]() 轴的交点为
轴的交点为![]() ,动点
,动点![]() 满足
满足![]() 平行于
平行于![]() 轴,且
轴,且![]() .
.
(1)求出![]() 点的轨迹方程.
点的轨迹方程.
(2)设点![]() ,
,![]() ,求
,求![]() 的最小值,并写出此时
的最小值,并写出此时![]() 点的坐标.
点的坐标.
(3)过点![]() 的直线与
的直线与![]() 点的轨迹交于
点的轨迹交于![]() .
.![]() 两点,求证
两点,求证![]() .
.![]() 两点的横坐标乘积为定值.
两点的横坐标乘积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),
的左侧),![]() 、
、![]() 是分别过
是分别过![]() 、
、![]() 点的圆
点的圆![]() 的切线,过此圆上的另一个点
的切线,过此圆上的另一个点![]() (
(![]() 点是圆上任一不与
点是圆上任一不与![]() 、
、![]() 重合的动点)作此圆的切线,分别交
重合的动点)作此圆的切线,分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 两直线交于点
两直线交于点![]() .
.
(![]() )设切点
)设切点![]() 坐标为
坐标为![]() ,求证:切线
,求证:切线![]() 的方程为
的方程为![]() .
.
(![]() )设点
)设点![]() 坐标为
坐标为![]() ,试写出
,试写出![]() 与
与![]() 的关系表达式(写出详细推理与计算过程).
的关系表达式(写出详细推理与计算过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com