Question

已知正四棱柱ABCD—A₁B₁C₁D₁中,AB=2,AA₁=4,E为BC的中点,F为直线CC₁上的动点,设=λ.

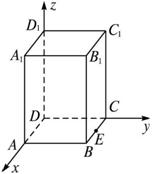
(1)当λ=3时,求EF与平面ABCD所成的角;

(2)当λ=1时,求二面角FDEC的大小(用反三角函数表示);

(3)当λ为何值时,有BD₁⊥EF?

Answer 1

解法一:(1)当λ=3时,CF=1.                                     

连结EF,EC为EF在平面ABCD上的射影,

∴∠FEC中就是EF与平面ABCD所成的角.                     

在Rt△FEC中,FC=EC=1,

∴∠FEC=45°.

∴EF与平面ABCD所成的角为45°.                             

(2)当λ=1时,CF=2.

过点C在平面ABCD中作CG⊥DE,垂足为G,连结FG,则FG⊥DE.

∴∠FGC就是二面角FDEC的平面角.                          

在Rt△FGC中,CG=,∴tan∠FGC=,                    

即二面角FDEC的大小为arctan.                           

(3)连结BC₁,BC₁为BD₁在平面B₁C₁CB上的射影.

要使BD₁⊥EF,只要EF⊥BC₁.                                 

过E点在平面B₁C₁CB上作EH⊥BC₁,垂足为H.HE与C₁C的延长线交于F.

此时△ECF∽△C₁CB,

∴=.∴CF=.                                     

∴当λ=-9时,BD₁⊥EF.                                       

解法二:(1)建立如图所示的空间直角坐标系,

则D(0,0,0),E(1,2,0).

当λ=3时,F(0,2,1),                                          

=(-1,0,1).

设平面ABCD的法向量为n,

则n=(0,0,1).

设与n的夹角为θ,

则cosθ==.                              

∴EF与平面ABCD所成的角为45°.                         

(2)当λ=1时,F(0,2,2),=(-1,0,2),=(0,2,2).            

设平面DEF的法向量为m,则m·=0,m·=0,

∴m=(2,-1,1).                                              

∴cos〈m,n〉==.                               

∴二面角FDEC的大小为arccos.                         

(3)显然D₁(0,0,4),B(2,2,0),设F(0,2,t),                          

则=(-1,0,t),=(-2,-2,4).                           

要使EF⊥BD₁,只要·=0,2+4t=0,t=-.             

∴λ=-9.