练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面，BC＝，M为BC的中点.

    （I）证明：AM⊥PM ；

    (II)求二面角P－AM－D的大小.

    【答案】（1）见解析； （2）45°.

    【解析】

    （Ⅰ）以D点为原点，分别以直线DA、DC为x轴、y轴，建立如图所示的空间直角坐标系,求出与的坐标，利用数量积为零，即可证得结果；（Ⅱ）求出平面PAM与平面ABCD的法向量，代入公式即可得到结果.

    （I）证明:以D点为原点，分别以直线DA、DC为x轴、y轴，建立如图所示的空间直角坐标系,依题意，可得

    ∴

    ∴

    即,∴AM⊥PM .

    (II)设，且平面PAM，则

    ,即 ∴ ,

    取，得；取，显然平面ABCD，

    ∴，结合图形可知，二面角P－AM－D为45°.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设有关于的一元二次方程．

    （Ⅰ）若是从四个数中任取的一个数，是从三个数中任取的一个数，求上述方程有实根的概率．

    （Ⅱ）若是从区间任取的一个数，是从区间任取的一个数，求上述方程有实根的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设的图像与y轴交点的纵坐标为1，在y轴右侧的第一个最大值和最小值分别为和.

    （1）求函数的解析式：

    （2）将函数图像上所有点的横坐标缩小原来的（纵坐标不变），再将所得图像沿x轴正方向平移个单位，得到函数的图像，求函数的解析式.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知角α＝45°，

    (1)在－720°～0°范围内找出所有与角α终边相同的角β；

    (2)设集合，判断两集合的关系．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，，对任意，有成立.

    （1）求的通项公式；

    （2）设，，是数列的前项和，求正整数，使得对任意，恒成立；

    （3）设，是数列的前项和，若对任意均有恒成立，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4—4：坐标系与参数方程

    已知曲线的参数方程为（为参数），以平面直角坐标系的原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为．

    （Ⅰ）求曲线的直角坐标方程及曲线上的动点到坐标原点的距离的最大值；

    （Ⅱ）若曲线与曲线相交于，两点，且与轴相交于点，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥P-ABC中，PA⊥底面ABC， .点D，E，N分别为棱PA，PC，BC的中点，M是线段AD的中点，PA=AC=4，AB=2.

    （Ⅰ）求证：MN∥平面BDE；

    （Ⅱ）求二面角C-EM-N的正弦值；

    （Ⅲ）已知点H在棱PA上，且直线NH与直线BE所成角的余弦值为，求线段AH的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某同学用“五点法”画函数在某一个周期内的图象时，列表并填入了部分数据，如下表：

    0

    π

    2π

    x

    0

    4

    -4

    0

    （1）请将上表数据补充完整，填写在答题卡上相应位置，并直接写出函数f（x）的解析式；

    （2）将图象上所有点向左平行移动θ（）个单位长度，得到的图象.若图象的一个对称中心为，求θ的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，直线l的参数方程为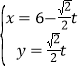（t是参数），在以坐标原点为极点，x轴的正半轴为极轴的极坐标系中，曲线C的极坐标方程为．

    （Ⅰ）写出直线l的普通方程、曲线C的参数方程；

    （Ⅱ）过曲线C上任意一点A作与直线l的夹角为45°的直线，设该直线与直线l交于点B，求的最值．

    查看答案和解析>>

    同步练习册答案