
ЁОЬтФПЁПЫцзХЛЅСЊЭјЕФЗЂеЙЃЌвЦЖЏжЇИЖЃЈгжГЦЪжЛњжЇИЖЃЉдНРДдНЦеБщЃЌФГбЇаЃаЫШЄаЁзщЮЊСЫСЫНтвЦЖЏжЇИЖдкДѓжкжаЕФЪьжЊЖШЃЌЖд15-65ЫъЕФШЫШКЫцЛњГщбљЕїВщЃЌЕїВщЕФЮЪЬтЪЧЁАФуЛсЪЙгУвЦЖЏжЇИЖТ№ЃПЁБЦфжаЃЌЛиД№ЁАЛсЁБЕФЙВга![]() ИіШЫЃЌАбет
ИіШЫЃЌАбет![]() ИіШЫАДееФъСфЗжГЩ5зщЃКЕк1зщ
ИіШЫАДееФъСфЗжГЩ5зщЃКЕк1зщ![]() ЃЌЕк2зщ
ЃЌЕк2зщ![]() ЃЌЕк3зщ
ЃЌЕк3зщ![]() ЃЌЕк4зщ
ЃЌЕк4зщ![]() ЃЌЕк5зщ
ЃЌЕк5зщ![]() ЃЌШЛКѓЛцжЦГЩШчЭМЫљЪОЕФЦЕТЪЗжВМжБЗНЭМЃЌЦфжаЃЌЕквЛзщЕФЦЕЪ§ЮЊ20.
ЃЌШЛКѓЛцжЦГЩШчЭМЫљЪОЕФЦЕТЪЗжВМжБЗНЭМЃЌЦфжаЃЌЕквЛзщЕФЦЕЪ§ЮЊ20.

ЃЈ1ЃЉЧѓ![]() КЭ
КЭ![]() ЕФжЕЃЌВЂИљОнЦЕТЪЗжВМжБЗНЭМЙРМЦетзщЪ§ОнЕФжкЪ§ЃЛ
ЕФжЕЃЌВЂИљОнЦЕТЪЗжВМжБЗНЭМЙРМЦетзщЪ§ОнЕФжкЪ§ЃЛ
ЃЈ2ЃЉДгЕк1ЃЌ3ЃЌ4зщжагУЗжВуГщбљЕФЗНЗЈГщШЁ6ШЫЃЌЧѓЕк1ЃЌ3ЃЌ4зщГщШЁЕФШЫЪ§ЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉГщШЁЕФ6ШЫжадйЫцЛњГщШЁ2ШЫЃЌЧѓЫљГщШЁЕФ2ШЫРДздЭЌвЛИізщЕФИХТЪ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЌжкЪ§ЮЊ30ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉ
ЃЌжкЪ§ЮЊ30ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЦЕТЪЁЂЦЕЪ§КЭбљБОШнСПЕФЙиЯЕКЭЕквЛзщЕФЦЕЪ§ПЩЕУ![]() ЃЌШЛКѓИљОнЫљгааЁГЄЗНаЮЕФУцЛ§КЭЮЊ1ЧѓГі
ЃЌШЛКѓИљОнЫљгааЁГЄЗНаЮЕФУцЛ§КЭЮЊ1ЧѓГі![]() ЃЎЃЈ2ЃЉЯШЧѓГіГщбљБШР§ЃЌШЛКѓИљОнЗжВуГщбљЕФВНжшНјааЧѓНтМДПЩЃЎЃЈ3ЃЉСаОйЕУЕНЯргІЕФЪТМўЕФИіЪ§ЃЌдйИљОнЙХЕфИХаЭИХТЪЙЋЪНЧѓНтЃЎ
ЃЎЃЈ2ЃЉЯШЧѓГіГщбљБШР§ЃЌШЛКѓИљОнЗжВуГщбљЕФВНжшНјааЧѓНтМДПЩЃЎЃЈ3ЃЉСаОйЕУЕНЯргІЕФЪТМўЕФИіЪ§ЃЌдйИљОнЙХЕфИХаЭИХТЪЙЋЪНЧѓНтЃЎ
ЃЈ1ЃЉгЩЬтвтПЩжЊЃЌ![]() ЃЌ
ЃЌ
гЩ![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
гЩЦЕТЪЗжВМжБЗНЭМПЩЙРМЦетзщЪ§ОнЕФжкЪ§ЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЕк1ЃЌ3ЃЌ4зщЦЕТЪжЎБШЮЊ0.020ЃК0.030ЃК0.010=2ЃК3ЃК1
дђДгЕк1зщГщШЁЕФШЫЪ§ЮЊ![]() ЃЌ
ЃЌ
ДгЕк3зщГщШЁЕФШЫЪ§ЮЊ![]() ЃЌ
ЃЌ
ДгЕк4зщГщШЁЕФШЫЪ§ЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЩшЕк1зщГщШЁЕФ2ШЫЮЊ![]() ЃЌЕк3зщГщШЁЕФ3ШЫЮЊ
ЃЌЕк3зщГщШЁЕФ3ШЫЮЊ![]() ЃЌЕк4зщГщШЁЕФ1ШЫЮЊ
ЃЌЕк4зщГщШЁЕФ1ШЫЮЊ![]() ЃЌдђДгет6ШЫжаЫцЛњГщШЁ2ШЫгаШчЯТжжЧщаЮЃК
ЃЌдђДгет6ШЫжаЫцЛњГщШЁ2ШЫгаШчЯТжжЧщаЮЃК![]()
![]() ЃЌЙВга15ИіЛљБОЪТМўЃЌЦфжаЗћКЯЁАГщШЁЕФ2ШЫРДздЭЌвЛИізщЁБЕФЛљБОЪТМўга
ЃЌЙВга15ИіЛљБОЪТМўЃЌЦфжаЗћКЯЁАГщШЁЕФ2ШЫРДздЭЌвЛИізщЁБЕФЛљБОЪТМўга![]() ЙВ4ИіЛљБОЪТМўЃЌ
ЙВ4ИіЛљБОЪТМўЃЌ
ЫљвдГщШЁЕФ2ШЫРДздЭЌвЛИізщЕФИХТЪЮЊ![]() ЃЎ
ЃЎ


 ПЮЪБбЕСЗНЫеШЫУёГіАцЩчЯЕСаД№АИ
ПЮЪБбЕСЗНЫеШЫУёГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋКЏЪ§ ![]() ЭМЯёЩЯЕФЕуPЃЈ
ЭМЯёЩЯЕФЕуPЃЈ ![]() ЃЌt ЃЉЯђзѓЦНвЦsЃЈsЉ0ЃЉ ИіЕЅЮЛГЄЖШЕУЕНЕуPЁф.Шє PЁфЮЛгкКЏЪ§y=sin2xЕФЭМЯёЩЯЃЌдђ( )
ЃЌt ЃЉЯђзѓЦНвЦsЃЈsЉ0ЃЉ ИіЕЅЮЛГЄЖШЕУЕНЕуPЁф.Шє PЁфЮЛгкКЏЪ§y=sin2xЕФЭМЯёЩЯЃЌдђ( )
A.t= ![]() ЃЌsЕФзюаЁжЕЮЊ
ЃЌsЕФзюаЁжЕЮЊ ![]()
B.t= ![]() ЃЌsЕФзюаЁжЕЮЊ
ЃЌsЕФзюаЁжЕЮЊ ![]()
C.t= ![]() ЃЌsЕФзюаЁжЕЮЊ
ЃЌsЕФзюаЁжЕЮЊ ![]()
D.t= ![]() ЃЌsЕФзюаЁжЕЮЊ
ЃЌsЕФзюаЁжЕЮЊ ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖPЃABCDжаЃЌPAЁЭЕзУцABCDЃЌADЁЭABЃЌABЁЮDCЃЌADЃНDCЃНAPЃН2ЃЌABЃН1ЃЌЕуEЮЊРтPCЕФжаЕуЃЎ

(1)жЄУїЃКBEЁЭDCЃЛ
(2)ЧѓжБЯпBEгыЦНУцPBDЫљГЩНЧЕФе§ЯвжЕЃЛ
(3)ШєFЮЊРтPCЩЯвЛЕуЃЌТњзуBFЁЭACЃЌЧѓЖўУцНЧFЃABЃPЕФгрЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§fЃЈxЃЉ=x3ЉaxЉbЃЌxЁЪRЃЌЦфжаaЃЌbЁЪRЃЎ
ЃЈ1ЃЉЧѓfЃЈxЃЉЕФЕЅЕїЧјМфЃЛ
ЃЈ2ЃЉШєfЃЈxЃЉДцдкМЋжЕЕуx0 ЃЌ ЧвfЃЈx1ЃЉ=fЃЈx0ЃЉЃЌЦфжаx1Ёйx0 ЃЌ ЧѓжЄЃКx1+2x0=0ЃЛ
ЃЈ3ЃЉЩшaЃО0ЃЌКЏЪ§gЃЈxЃЉ=|fЃЈxЃЉ|ЃЌЧѓжЄЃКgЃЈxЃЉдкЧјМф[Љ1ЃЌ1]ЩЯЕФзюДѓжЕВЛаЁгк ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєКЏЪ§y=fЃЈxЃЉЕФЭМЯѓЩЯДцдкСНЕуЃЌЪЙЕУКЏЪ§ЕФЭМЯѓдкетСНЕуДІЕФЧаЯпЛЅЯрДЙжБЃЌдђГЦy=fЃЈxЃЉОпгаTаджЪЃЎЯТСаКЏЪ§жаОпгаTаджЪЕФЪЧЃЈЁЁЁЁЃЉ
A.y=sinx
B.y=lnx
C.y=ex
D.y=x3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
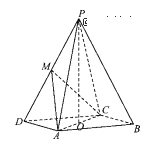
ЁОЬтФПЁПдкЫФРтзЖP-ABCжаЃЌЕзУцABCDЮЊЦНааЫФБпаЮЃЌ![]() ЃЌOЮЊACЕФжаЕуЃЌ
ЃЌOЮЊACЕФжаЕуЃЌ![]() ЦНУц
ЦНУц![]() MЮЊPDЕФжаЕуЁЃ
MЮЊPDЕФжаЕуЁЃ
ЃЈ1ЃЉжЄУї![]() ЦНУц
ЦНУц![]() ЃЎ
ЃЎ
ЃЈ2ЃЉжЄУї![]() ЦНУц
ЦНУц![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЧѓШ§РтзЖP-MACЬхЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЃК
ЃК ![]() ЃЈ
ЃЈ![]() ЃЉЕФЭЈОЖЃЈЙ§НЙЕуЧвДЙжБгкЖдГЦжсЕФЯвЃЉГЄЮЊ
ЃЉЕФЭЈОЖЃЈЙ§НЙЕуЧвДЙжБгкЖдГЦжсЕФЯвЃЉГЄЮЊ![]() ЃЌЭждВ
ЃЌЭждВ![]() ЃК
ЃК ![]() ЃЈ
ЃЈ![]() ЃЉЕФРыаФТЪЮЊ
ЃЉЕФРыаФТЪЮЊ![]() ЃЌЧвЙ§ХзЮяЯп
ЃЌЧвЙ§ХзЮяЯп![]() ЕФНЙЕу.
ЕФНЙЕу.

ЃЈ1ЃЉЧѓХзЮяЯп![]() КЭЭждВ
КЭЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЙ§ЖЈЕу![]() в§жБЯп
в§жБЯп![]() НЛХзЮяЯп
НЛХзЮяЯп![]() гк
гк![]() ЁЂ
ЁЂ![]() СНЕуЃЈ
СНЕуЃЈ![]() дк
дк![]() ЕФзѓВрЃЉЃЌЗжБ№Й§
ЕФзѓВрЃЉЃЌЗжБ№Й§![]() ЁЂ
ЁЂ![]() зїХзЮяЯп
зїХзЮяЯп![]() ЕФЧаЯп
ЕФЧаЯп![]() ЃЌ
ЃЌ ![]() ЃЌЧв
ЃЌЧв![]() гыЭждВ
гыЭждВ![]() ЯрНЛгк
ЯрНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌМЧДЫЪБСНЧаЯп
СНЕуЃЌМЧДЫЪБСНЧаЯп![]() ЃЌ
ЃЌ ![]() ЕФНЛЕуЮЊ
ЕФНЛЕуЮЊ![]() .
.
ЂйЧѓЕу![]() ЕФЙьМЃЗНГЬЃЛ
ЕФЙьМЃЗНГЬЃЛ
ЂкЩшЕу![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФУцЛ§ЕФзюДѓжЕЃЌВЂЧѓГіДЫЪБ
ЕФУцЛ§ЕФзюДѓжЕЃЌВЂЧѓГіДЫЪБ![]() ЕуЕФзјБъ.
ЕуЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЄГЇЮЊСЫЖдаТбаЗЂЕФвЛжжВњЦЗНјааКЯРэЖЈМлЃЌНЋИУВњЦЗАДЪТЯШФтЖЈЕФМлИёНјааЪдЯњЃЌЕУЕНШчЯТЪ§ОнЃК
ЕЅМлx(дЊ) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
ЯњСПy(Мў) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)ЧѓЛиЙщжБЯпЗНГЬ![]() ЃНbxЃЋaЃЛЃЈЦфжа
ЃНbxЃЋaЃЛЃЈЦфжа ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
(2)дЄМЦдкНёКѓЕФЯњЪлжаЃЌЯњСПгыЕЅМлШдШЛЗўДг(1)жаЕФЙиЯЕЃЌЧвИУВњЦЗЕФГЩБОЪЧ4дЊ/МўЃЌЮЊЪЙЙЄГЇЛёЕУзюДѓРћШѓЃЌИУВњЦЗЕФЕЅМлгІЖЈЮЊЖрЩйдЊЃП(РћШѓЃНЯњЪлЪеШыЃГЩБО)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=![]() ЃЎ
ЃЎ
ЃЈЂёЃЉЧѓКЏЪ§fЃЈxЃЉЕФЖЈвхгђЃЛ
ЃЈЂђЃЉХаЖЈfЃЈxЃЉЕФЦцХМадВЂжЄУїЃЛ
ЃЈЂѓЃЉгУКЏЪ§ЕЅЕїадЖЈвхжЄУїЃКfЃЈxЃЉдкЃЈ1ЃЌ+ЁоЃЉЩЯЪЧдіКЏЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com