
【题目】为庆祝国庆,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(成绩均为整数)分成六段![]() ,
,![]() ,…,
,…,![]() 后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题:

(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
【答案】(1)0.3;(2)及格率75%,平均分71.
【解析】
试题分析:(1)根据频率分布直方图的性质可知:每个小长方形的面积等于该组的频率,且所有小长方形的面积的和等于频率之和,等于1,所以第四组的频率等于1-(0.025+0.015+0.015+0.01+0.005)×10=0.3,所以第四组的频率为0.3,第四组的小长方形高为0.03,补全的频率分布直方图如下图;(2)60分及以上为第三、四、五、六组,根据频率分布直方图可知这四组的频率之和为1-(0.01+0.015)×10=0.75,所以估计本次考试的及格率为0.75,即75%,利用频率分布直方图可以估计出样本数据的平均值,具体计算方法是:用每一组数据的中点值乘以该组的频率,然后再相加,就可以得到平均值,所以本次考试的平均分为:45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71,所以根据频率分布直方图估算出的平均分为71分。
试题解析:(1)因为各组的频率和等于1,故第四组的频率:
![]() .
.
直方图如图所示.

{2}依题意,及格以上的分数所在的第三、四、五、六组的频率之和为
![]() ,
,
抽样学生成绩的合格率是75%.利用组中值估算抽样学生的平均分
![]()
则估计这次考试的平均分是71分


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:高中数学 来源: 题型:
【题目】已知直线![]() ,半径为
,半径为![]() 的圆
的圆![]() 与
与![]() 相切,圆心
相切,圆心![]() 在
在![]() 轴上且在直线
轴上且在直线![]() 的右上方.
的右上方.
(1)求圆的方程;
(2)若直线过点![]() 且与圆
且与圆![]() 交于
交于![]() 两点(
两点(![]() 在
在![]() 轴上方,B在
轴上方,B在![]() 轴下方),问在
轴下方),问在![]() 轴正半轴上是否存在定点
轴正半轴上是否存在定点![]() ,使得
,使得![]() 轴平分
轴平分![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.
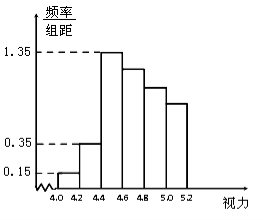
(1)若直方图中后四组的频数成等差数列,试估计全年级视力在5.0以下的人数;
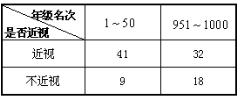
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到右表中数据,根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50的学生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:

![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地空气中出现污染,须喷洒一定量的去污剂进行处理.据测算,每喷洒![]() 个单位的去污剂,空气中释放的浓度
个单位的去污剂,空气中释放的浓度![]() (单位:毫克/立方米)随着时间
(单位:毫克/立方米)随着时间![]() 单位:天)变化的函数关系式,近似为
单位:天)变化的函数关系式,近似为
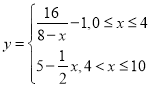 ,若多次喷洒,则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和. 由实验知,当空气中去污剂的浓度不低于
,若多次喷洒,则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和. 由实验知,当空气中去污剂的浓度不低于![]() (毫克/立方米)时,它才能起到去污作用.
(毫克/立方米)时,它才能起到去污作用.
(1)若一次喷洒![]() 个单位的去污剂,则去污时间可达几天?
个单位的去污剂,则去污时间可达几天?
(2)若第一次喷洒![]() 个单位的去污剂,
个单位的去污剂,![]() 天后再唢洒
天后再唢洒![]() 个单位的去污剂,要使接来的
个单位的去污剂,要使接来的![]() 天中能够持续有效去污,试求
天中能够持续有效去污,试求![]() 的最小值(精确到
的最小值(精确到![]() ,参考数据:
,参考数据:![]() 取
取![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与圆
与圆![]() :
:![]() 关于直线
关于直线![]() 对称,且点
对称,且点![]() 在圆
在圆![]() 上.
上.
(1)判断圆![]() 与圆
与圆![]() 的位置关系;
的位置关系;
(2)设![]() 为圆
为圆![]() 上任意一点,
上任意一点,![]() ,
,![]() ,
,![]() 三点不共线,
三点不共线,![]() 为
为![]() 的平分线,且交
的平分线,且交![]() 于
于![]() . 求证:
. 求证:![]() 与
与![]() 的面积之比为定值.
的面积之比为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题“如果一个四边形是正方形,那么这个四边形一定是矩形”及其逆命题、否命题、逆否命题,这四个命题中假命题的个数( )
A. 0 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com