
一个数字生成器,生成规则如下:第1次生成一个数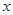 ,以后每次生成的结果是将上一次生成的每一个数
,以后每次生成的结果是将上一次生成的每一个数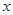 生成两个数,一
生成两个数,一
个是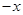 ,另一个是
,另一个是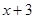 .设第
.设第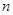 次生成的数的个数为
次生成的数的个数为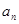 ,
,
则数列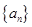 的前
的前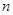 项和
项和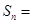 ;若
;若 ,前
,前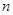 次
次
生成的所有数中不同的数的个数为 ,则
,则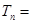 .
.
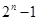 ,
,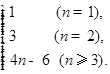
解析(1)根据题意,一个数字生成器,生成规则可得:第1次生成1个数,第二次生成2个数,第三次生成4个数,第四次生成8个数…,以此类推知该数列是等比数列,利用等比数列求和公式即可求出数列{an}的前n项和Sn
(2)因为一个数字生成器,生成规则如下:第1次生成一个数x,以后每次生成的结果是将上一次生成的每一个数x生成两个数,一个是-x,另一个是x+3,类推可求出数列的和.
解:(1)根据题意,一个数字生成器,生成规则可得:第1次生成1个数,第二次生成2个数,第三次生成4个数,第四次生成8个数…,以此类推,第n次生成的数的个数为an=2n-1,
显然,此数列为首项为1,公比为2的等比数列.再根据等比数列求和公式,则数列{an}的前n项和
Sn=2n-1.
(2)因为一个数字生成器,生成规则如下:第1次生成一个数x,以后每次生成的结果是将上一次生成的每一个数x生成两个数,一个是-x,另一个是x+3.
第一次生成的数为“1”,
第二次生成的数为“-1、4”,
第三次生成的数为“1、2、-4、7”,
第四次生成的数为“-1、4、-2、5、4、-1、-7、10”
…
可观察出:
第一次生成后前1次所有数中不同的个数为“1”,
第2次生成后前2次所有数中不同的个数为“3”,
第三次生成后前3次所有数中不同的个数为“6”,
第四次生成后前4次所有数中不同的个数为“10”,
…
以此类推以后为公差为4的等差数列.则易得数中不同的数的个数为Tn,则Tn=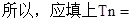


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010年北京市朝阳区高三下学期一模数学(文)测试 题型:填空题
一个数字生成器,生成规则如下:第1次生成一个数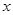 ,以后每次生成的结果可将上一次生成的每一个数
,以后每次生成的结果可将上一次生成的每一个数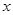 生成两个数,一个是
生成两个数,一个是
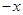 ,另一个是
,另一个是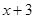 .设第
.设第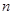 次生成的数的个数为
次生成的数的个数为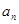 ,则数列
,则数列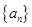 的前
的前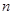 项和
项和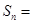 _________________;若
_________________;若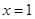 ,前
,前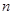 次生成的所有数中不同的数的个数为
次生成的所有数中不同的数的个数为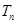 ,则
,则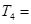 ______________________.
______________________.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年北京师大附中高一(下)期末数学试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com