Question

设t≠0,点P(t,0)是函数f(x)=x³+ax与g(x)=bx²+c的图象的一个公共点,两函数的图象在点P处有相同的切线.

(1)用t表示a、b、c;

(2)若函数y=f(x)-g(x)在(-1,3)上单调递减,求t的取值范围.

Answer 1

(1)解:因为函数f(x)、g(x)的图象都过点(t,0),

    所以f(t)=0,即t³+at=0.

    因为t≠0,所以a=-t².

    g(t)=0,即bt²+c=0,所以c=ab.

    又因为f(x)、g(x)在点(t,0)处有相同的切线,所以f′(t)=g′(t).

    而f′(x)=3x²+a,g′(x)=2bx,

    所以3t²+a=2bt.

    将a=-t²代入上式得b=t.

    因此c=ab=-t³.

    故a=-t²,b=t,c=-t³.

(2)解法一:y=f(x)-g(x)=x³-t²x-tx²+t³,y′=3x²-2tx-t²=(3x+t)(x-t).

    当y′=(3x+t)(x-t)＜0时,函数y=f(x)-g(x)单调递减.

    由y′＜0,若t＞0,则-＜x＜t;

    若t＜0,则t＜x＜-.

    由题意,函数y=f(x)-g(x)在(-1,3)上单调递减,则(-1,3)(-,t)或(-1,3)(t,-).

    所以t≥3或-≥3,即t≤-9或t≥3.

    又当-9＜t＜3时,函数y=f(x)-g(x)在(-1,3)上不单调递减.

    所以t的取值范围为(-∞,-9)∪［3,+∞).

    解法二:y=f(x)-g(x)=x³-t²x-tx²+t³,

    y′=3x²-2tx-t²=(3x+t)(x-t).

    因为函数y=f(x)-g(x)在(-1,3)上单调递减,且y′=(3x+t)(x-t)是开口向上的抛物线,

    所以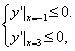

    即

    解得t≤-9或t≥3.

    所以t的取值范围为(-∞,-9)∪［3,+∞).