
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:ρsin2θ=2acosθ(a>0),直线l的参数方程为  (t为参数),l与C分别交于M,N,P(﹣2,﹣4).
(t为参数),l与C分别交于M,N,P(﹣2,﹣4).
(1)写出C的平面直角坐标系方程和l的普通方程;
(2)已知|PM|,|MN|,|PN|成等比数列,求a的值.
【答案】
(1)解:曲线C:ρsin2θ=2acosθ(a>0),即ρ2sin2θ=2aρcosθ(a>0),可得直角坐标方程:y2=2ax(a>0).
直线l的参数方程为 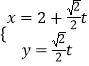 (t为参数),化为普通方程:y=x﹣2
(t为参数),化为普通方程:y=x﹣2
(2)解:点P(﹣2,﹣4)在直线l上,可得直线l的标准方程:  ,代入抛物线方程可得:m2﹣
,代入抛物线方程可得:m2﹣ ![]() m+4a+32=0,
m+4a+32=0,
△= ![]() ﹣4(4a+32)=2a2+16a>0,(a>0).
﹣4(4a+32)=2a2+16a>0,(a>0).
∴m1+m2= ![]() ,m1m2=4a+32.
,m1m2=4a+32.
|PM|=m1,|PN|=m2,|MN|=|m1﹣m2|= ![]() =
= ![]() =
= ![]() .
.
∵|PM|,|MN|,|PN|成等比数列,
∴|MN|2=|PM||PN|,
∴2a2+16a=m1m2=4a+32,化为:a2+6a﹣16=0,a>0,
解得a=2.
【解析】(1)曲线C:ρsin2θ=2acosθ(a>0),即ρ2sin2θ=2aρcosθ(a>0),把x=ρcosθ,y=ρsinθ代入即可得出直角坐标方程.直线l的参数方程为 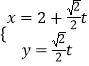 (t为参数),消去参数t化为普通方程:y=x﹣2.(2)点P(﹣2,﹣4)在直线l上,可得直线l的标准方程:
(t为参数),消去参数t化为普通方程:y=x﹣2.(2)点P(﹣2,﹣4)在直线l上,可得直线l的标准方程:  ,代入抛物线方程可得:m2﹣
,代入抛物线方程可得:m2﹣ ![]() m+4a+32=0,|PM|=m1 , |PN|=m2 , |MN|=|m1﹣m2|=
m+4a+32=0,|PM|=m1 , |PN|=m2 , |MN|=|m1﹣m2|= ![]() ,由于|PM|,|MN|,|PN|成等比数列,可得|MN|2=|PM||PN|,即可得出.
,由于|PM|,|MN|,|PN|成等比数列,可得|MN|2=|PM||PN|,即可得出.


科目:高中数学 来源: 题型:
【题目】已知函数 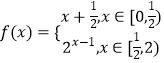 ,若存在x1 , x2 , 当0≤x1<x2<2时,f(x1)=f(x2),则x1f(x2)﹣f(x2)的取值范围为( )
,若存在x1 , x2 , 当0≤x1<x2<2时,f(x1)=f(x2),则x1f(x2)﹣f(x2)的取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨,生产每吨乙产品要用A原料1吨,B原料3吨。销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元,该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨,那么该企业可获得最大利润是___________万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点
的右焦点![]() ,过点
,过点![]() 且与坐标轴不垂直的直线与椭圆交于
且与坐标轴不垂直的直线与椭圆交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 经过椭圆的一个顶点时其倾斜角恰好为
经过椭圆的一个顶点时其倾斜角恰好为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,线段
为坐标原点,线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积= ![]() (弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为
(弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为 ![]() ,半径等于4米的弧田,按照上述经验公式计算所得弧田面积约是( )
,半径等于4米的弧田,按照上述经验公式计算所得弧田面积约是( ) 
A.6平方米
B.9平方米
C.12平方米
D.15平方米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,PA=AC=2,E是PC的中点,∠DAC=∠AOB 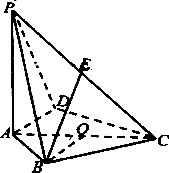
(1)求证:BE∥平面PAD;
(2)若二面角P﹣CD﹣A的正切值为2,求直线PB与平面PCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A1B1C1D1中,M、N、E、F分别是棱A1B1、A1D1、B1C1、C1D1的中点.
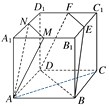
(1)求MN与AC所成角,并说明理由.
(2)求证:平面AMN∥平面EFDB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com