
ЎҫМвДҝЎҝТСЦӘФІҫЯУРТФПВРФЦКЈәЙиAЈ¬BКЗФІCЈә![]() ЙП№ШУЪФӯөг¶ФіЖөДБҪөгЈ¬өгPКЗФІЙПөДИОТвТ»өгЈ®ИфЦұПЯPAЈ¬PBөДРұВК¶јҙжФЪІў·ЦұрјЗОӘ
ЙП№ШУЪФӯөг¶ФіЖөДБҪөгЈ¬өгPКЗФІЙПөДИОТвТ»өгЈ®ИфЦұПЯPAЈ¬PBөДРұВК¶јҙжФЪІў·ЦұрјЗОӘ![]() Ј¬
Ј¬![]() Ј¬Фт
Ј¬Фт![]() ЈҪ©Ғ1Ј¬КЗУлөгPөДО»ЦГОЮ№ШөД¶ЁЦөЈ®
ЈҪ©Ғ1Ј¬КЗУлөгPөДО»ЦГОЮ№ШөД¶ЁЦөЈ®
ЈЁ1Ј©КФАаұИФІөДЙПКцРФЦКЈ¬РҙіцНЦФІ![]() өДТ»ёцАаЛЖРФЦКЈ¬ІўјУТФЦӨГчЈ»
өДТ»ёцАаЛЖРФЦКЈ¬ІўјУТФЦӨГчЈ»
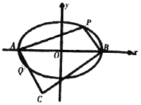
ЈЁ2Ј©ИзНјЈ¬ИфНЦФІMөДұкЧј·ҪіМОӘ![]() Ј¬өгPФЪНЦФІMЙПЗТО»УЪөЪТ»ПуПЮЈ¬өгAЈ¬B·ЦұрОӘНЦФІіӨЦбөДБҪёц¶ЛөгЈ¬№эөгAЈ¬B·ЦұрЧч
Ј¬өгPФЪНЦФІMЙПЗТО»УЪөЪТ»ПуПЮЈ¬өгAЈ¬B·ЦұрОӘНЦФІіӨЦбөДБҪёц¶ЛөгЈ¬№эөгAЈ¬B·ЦұрЧч![]() ЎНPAЈ¬
ЎНPAЈ¬![]() ЎНPBЈ¬ЦұПЯ
ЎНPBЈ¬ЦұПЯ![]() Ј¬
Ј¬![]() Ҫ»УЪөгCЈ¬ЦұПЯ
Ҫ»УЪөгCЈ¬ЦұПЯ![]() УлНЦФІMөДБнТ»Ҫ»өгОӘQЈ¬ЗТ
УлНЦФІMөДБнТ»Ҫ»өгОӘQЈ¬ЗТ![]() Ј¬Зу
Ј¬Зу![]() өДИЎЦө·¶О§ЈЁҝЙЦұҪУК№УГЈЁ1Ј©ЦРЦӨГчөДҪбВЫЈ©Ј®
өДИЎЦө·¶О§ЈЁҝЙЦұҪУК№УГЈЁ1Ј©ЦРЦӨГчөДҪбВЫЈ©Ј®
Ўҫҙр°ёЎҝЈЁ1Ј©јыЦӨГчЈ»ЈЁ2Ј©![]()
ЎҫҪвОцЎҝ
ЈЁ1Ј©Йиөг![]() Ј¬Фтөг
Ј¬Фтөг![]() Ј¬УЙ
Ј¬УЙ![]() Ј¬УЙНЦФІ·ҪіМҙшИл»ҜјтҝЙөГҪвЈ»
Ј¬УЙНЦФІ·ҪіМҙшИл»ҜјтҝЙөГҪвЈ»
ЈЁ2Ј©ЙиAPөДРұВКОӘkЈ¬![]() Ј¬ҪбәПЈЁ1Ј©ЦРөДҪбВЫҝЙөГЦұПЯACЎўBCәНBQөД·ҪіМЈ¬БӘБўЦұПЯ·ҪіМҝЙөГ
Ј¬ҪбәПЈЁ1Ј©ЦРөДҪбВЫҝЙөГЦұПЯACЎўBCәНBQөД·ҪіМЈ¬БӘБўЦұПЯ·ҪіМҝЙөГ![]() әН
әН![]() Ј¬УЙ
Ј¬УЙ![]() Ј¬ҪбәП
Ј¬ҪбәП![]() ҝЙөГҪв.
ҝЙөГҪв.
ЈЁ1Ј©РФЦКЈәЙиAЈ¬BКЗНЦФІ![]() ЙП№ШУЪФӯөг¶ФіЖөДБҪөгЈ¬өг
ЙП№ШУЪФӯөг¶ФіЖөДБҪөгЈ¬өг![]() КЗНЦФІЙПөДИОТвТ»өгЈ®ИфЦұПЯ
КЗНЦФІЙПөДИОТвТ»өгЈ®ИфЦұПЯ![]() Ј¬
Ј¬![]() өДРұВК¶јҙжФЪІў·ЦұрјЗОӘ
өДРұВК¶јҙжФЪІў·ЦұрјЗОӘ![]() Ј¬
Ј¬![]() Ј¬Фт
Ј¬Фт![]() КЗУлөг
КЗУлөг![]() өДО»ЦГОЮ№ШөД¶ЁЦөЈ®
өДО»ЦГОЮ№ШөД¶ЁЦөЈ®
ЦӨГчЈәЙиөг![]() Ј¬Фтөг
Ј¬Фтөг![]() Ј¬ҙУ¶ш
Ј¬ҙУ¶ш![]() Ј®Йиөг
Ј®Йиөг![]() Фт
Фт![]() Ј¬
Ј¬
Фт Ј¬
Ј¬
№К![]() КЗУлөгPөДО»ЦГОЮ№ШөД¶ЁЦөЈ®
КЗУлөгPөДО»ЦГОЮ№ШөД¶ЁЦөЈ®
ЈЁ2Ј©ЙиAPөДРұВКОӘkЈ¬![]() Ј¬ТтОӘPОӘНЦФІMЙПөЪТ»ПуПЮДЪТ»өгЈ¬ЛщТФ
Ј¬ТтОӘPОӘНЦФІMЙПөЪТ»ПуПЮДЪТ»өгЈ¬ЛщТФ![]() УЙЈЁ1Ј©ҪбВЫҝЙЦӘ
УЙЈЁ1Ј©ҪбВЫҝЙЦӘ![]() Ј¬ЛщТФBPөДРұВКОӘ
Ј¬ЛщТФBPөДРұВКОӘ![]() Ј®
Ј®
ТтОӘ![]() Ј¬ЛщТФ
Ј¬ЛщТФ![]() Ј¬ФтACөД·ҪіМОӘ
Ј¬ФтACөД·ҪіМОӘ![]()
ТтОӘ![]() Ј¬ЛщТФ
Ј¬ЛщТФ![]() Ј¬ФтBCөД·ҪіМОӘ
Ј¬ФтBCөД·ҪіМОӘ![]() .
.
УЙ Ј¬өГ
Ј¬өГ![]() Ј¬јҙ
Ј¬јҙ![]()
Йи![]() Ј¬ТтОӘ
Ј¬ТтОӘ![]() Ј¬
Ј¬
ЗТЦұПЯ![]() өДРұВК
өДРұВК![]() Ј¬ЛщТФ
Ј¬ЛщТФ![]() өДРұВКОӘ
өДРұВКОӘ![]() Ј¬Фт
Ј¬Фт![]() өД·ҪіМОӘ
өД·ҪіМОӘ![]()
БӘБў·ҪіМ Ј¬өГ
Ј¬өГ![]() Ј¬јҙ
Ј¬јҙ![]()
Фт
ТтОӘ![]() Ј¬ЛщТФ
Ј¬ЛщТФ![]() .
.


 ГыКҰЦёөјЖЪД©іеҙМҫнПөБРҙр°ё
ГыКҰЦёөјЖЪД©іеҙМҫнПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝПЦҙУДіТҪФәЦРЛж»ъійИЎБЛЖЯО»ТҪ»ӨИЛФұөД№Ш°®»јХЯҝјәЛ·ЦКэЈЁ»јХЯҝјәЛЈә10·ЦЦЖЈ©Ј¬УГПа№ШөДМШХчБҝ![]() ұнКҫЈ»ТҪ»ӨЧЁТөЦӘК¶ҝјәЛ·ЦКэЈЁКФҫнҝјКФЈә100·ЦЦЖЈ©Ј¬УГПа№ШөДМШХчБҝ
ұнКҫЈ»ТҪ»ӨЧЁТөЦӘК¶ҝјәЛ·ЦКэЈЁКФҫнҝјКФЈә100·ЦЦЖЈ©Ј¬УГПа№ШөДМШХчБҝ![]() ұнКҫЈ¬КэҫЭИзПВұнЈә
ұнКҫЈ¬КэҫЭИзПВұнЈә
ЈЁўсЈ©Зу![]() №ШУЪ
№ШУЪ![]() өДПЯРФ»Ш№й·ҪіМЈЁјЖЛгҪб№ыҫ«И·өҪ0.01Ј©Ј»
өДПЯРФ»Ш№й·ҪіМЈЁјЖЛгҪб№ыҫ«И·өҪ0.01Ј©Ј»
ЈЁўтЈ©АыУГЈЁIЈ©ЦРөДПЯРФ»Ш№й·ҪіМЈ¬·ЦОцТҪ»ӨЧЁТөҝјәЛ·ЦКэөДұд»Ҝ¶Ф№Ш°®»јХЯҝјәЛ·ЦКэөДУ°ПмЈ¬Іў№АјЖДіТҪ»ӨИЛФұөДТҪ»ӨЧЁТөЦӘК¶ҝјәЛ·ЦКэОӘ95·ЦКұЈ¬ЛыөД№Ш°®»јХЯҝјәЛ·ЦКэЈЁҫ«И·өҪ0.1Ј©Ј»

ЈЁўуЈ©ПЦТӘҙУТҪ»ӨЧЁТөЦӘК¶ҝјәЛ·ЦКэ95·ЦТФПВөДТҪ»ӨИЛФұЦРСЎЕЙ2ИЛІОјУЧйҪЁөДЎ°ҫЕХҜ№өФЦәуТҪ»ӨРЎ·Ц¶УЎұЕаСөЈ¬ЗуХвБҪИЛЦРЦБЙЩУРТ»ИЛҝјәЛ·ЦКэФЪ90·ЦТФПВөДёЕВК.
ёҪЈә»Ш№й·ҪіМ![]() ЦРРұВКәНҪШҫаөДЧоРЎ¶юіЛ·Ё№АјЖ№«КҪ·ЦұрОӘ
ЦРРұВКәНҪШҫаөДЧоРЎ¶юіЛ·Ё№АјЖ№«КҪ·ЦұрОӘ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЈЁ12·ЦЈ©
ТСЦӘәҜКэ![]() ЈЁaОӘКөКэЈ©.
ЈЁaОӘКөКэЈ©.
ЈЁ1Ј©өұ![]() КұЈ¬ЗуәҜКэ
КұЈ¬ЗуәҜКэ![]() өДНјПсФЪ
өДНјПсФЪ![]() ҙҰөДЗРПЯ·ҪіМЈ»
ҙҰөДЗРПЯ·ҪіМЈ»
ЈЁ2Ј©Зу![]() ФЪЗшјд
ФЪЗшјд![]() ЙПөДЧоРЎЦөЈ»
ЙПөДЧоРЎЦөЈ»
ЈЁ3Ј©ИфҙжФЪБҪёцІ»өИКөКэ![]() Ј¬К№·ҪіМ
Ј¬К№·ҪіМ![]() іЙБўЈ¬ЗуКөКэaөДИЎЦө·¶О§.
іЙБўЈ¬ЗуКөКэaөДИЎЦө·¶О§.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіЧвБЮ№«ЛҫУөУРЖыіө100Бҫ.өұГҝБҫіөөДФВЧвҪрОӘ![]() ФӘКұЈ¬ҝЙИ«ІҝЧвіц.өұГҝБҫіөөДФВЧвҪрГҝФцјУ50ФӘКұЈ¬ОҙЧвіцөДіөҪ«»бФцјУТ»Бҫ.ЧвіцөДіөГҝБҫГҝФВРиТӘО¬»Ө·С150ФӘЈ¬ОҙЧвіцөДіөГҝБҫГҝФВРиТӘО¬»Ө·С50ФӘ.ИфК№ЧвБЮ№«ЛҫөДФВКХТжЧоҙуЈ¬ГҝБҫіөөДФВЧвҪрУҰёГ¶ЁОӘ__________Ј®
ФӘКұЈ¬ҝЙИ«ІҝЧвіц.өұГҝБҫіөөДФВЧвҪрГҝФцјУ50ФӘКұЈ¬ОҙЧвіцөДіөҪ«»бФцјУТ»Бҫ.ЧвіцөДіөГҝБҫГҝФВРиТӘО¬»Ө·С150ФӘЈ¬ОҙЧвіцөДіөГҝБҫГҝФВРиТӘО¬»Ө·С50ФӘ.ИфК№ЧвБЮ№«ЛҫөДФВКХТжЧоҙуЈ¬ГҝБҫіөөДФВЧвҪрУҰёГ¶ЁОӘ__________Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() Ј¬
Ј¬![]() Ј¬Иф
Ј¬Иф![]() УРЧоРЎЦөЈ¬ФтКөКэ
УРЧоРЎЦөЈ¬ФтКөКэ![]() өДИЎЦө·¶О§КЗЈЁ Ј©
өДИЎЦө·¶О§КЗЈЁ Ј©
A. ![]() B.
B. ![]() C.
C.  D.
D. 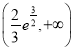
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬НЦФІ![]() Јә
Јә ![]() өДАлРДВКОӘ
өДАлРДВКОӘ![]() Ј¬өг
Ј¬өг![]() ФЪНЦФІ
ФЪНЦФІ![]() ЙПЈ®
ЙПЈ®
ЈЁ1Ј©ЗуНЦФІ![]() өД·ҪіМЈ»
өД·ҪіМЈ»
ЈЁ2Ј©ТСЦӘ![]() Ул
Ул![]() ОӘЖҪГжДЪөДБҪёц¶ЁөгЈ¬№э
ОӘЖҪГжДЪөДБҪёц¶ЁөгЈ¬№э![]() өгөДЦұПЯ
өгөДЦұПЯ![]() УлНЦФІ
УлНЦФІ![]() Ҫ»УЪ
Ҫ»УЪ![]() Ј¬
Ј¬ ![]() БҪөгЈ¬ЗуЛДұЯРО
БҪөгЈ¬ЗуЛДұЯРО![]() Гж»эөДЧоҙуЦөЈ®
Гж»эөДЧоҙуЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝіЗХт»ҜКЗ№ъјТПЦҙъ»ҜөДЦШТӘЦёұкЈ¬ҫЭУР№ШЧКБППФКҫЈ¬1978ЎӘ2013ДкЈ¬ОТ№ъіЗХтіЈЧЎИЛҝЪҙУ1.7ТЪФцјУөҪ7.3ТЪЈ®јЩЙиГҝТ»ДкіЗХтіЈЧЎИЛҝЪөДФцјУБҝ¶јПаөИЈ¬јЗ1978ДкәуөЪtЈЁПЮ¶Ё![]() Ј©ДкөДіЗХтіЈЧЎИЛҝЪОӘ
Ј©ДкөДіЗХтіЈЧЎИЛҝЪОӘ![]() ТЪЈ®Рҙіц
ТЪЈ®Рҙіц![]() өДҪвОцКҪЈ¬ІўУЙҙЛ№АЛгіцОТ№ъ2017ДкөДіЗХтіЈЧЎИЛҝЪКэЈ®
өДҪвОцКҪЈ¬ІўУЙҙЛ№АЛгіцОТ№ъ2017ДкөДіЗХтіЈЧЎИЛҝЪКэЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝХэ·ҪМе![]() өДАвіӨОӘ
өДАвіӨОӘ![]() Ј¬
Ј¬![]() ·ЦұрКЗ
·ЦұрКЗ![]() өДЦРөгЈ¬Фт№э
өДЦРөгЈ¬Фт№э![]() ЗТУл
ЗТУл![]() ЖҪРРөДЖҪГжҪШХэ·ҪМеЛщөГҪШГжөДГж»эОӘ____________
ЖҪРРөДЖҪГжҪШХэ·ҪМеЛщөГҪШГжөДГж»эОӘ____________
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪұҫКРДіҫЙРЎЗшёДФм№ӨіМЦРЈ¬РиТӘФЪөШПВЖМЙиМмИјЖш№ЬөА.ТСЦӘРЎЗшДіҙҰИэҙұ·ҝОЭ·ЦұрО»УЪЙИРО![]() өДИэёц¶ҘөгЙПЈ¬өг
өДИэёц¶ҘөгЙПЈ¬өг![]() КЗ»Ў
КЗ»Ў![]() өДЦРөгЈ¬ПЦУыФЪПЯ¶О
өДЦРөгЈ¬ПЦУыФЪПЯ¶О![]() ЙПХТТ»ҙҰҝӘНЪ№ӨЧчҝУ
ЙПХТТ»ҙҰҝӘНЪ№ӨЧчҝУ![]() ЈЁІ»Улөг
ЈЁІ»Улөг![]() Ј¬
Ј¬![]() ЦШәПЈ©Ј¬ОӘЖМЙиИэМхөШПВМмИјЖш№ЬПЯ
ЦШәПЈ©Ј¬ОӘЖМЙиИэМхөШПВМмИјЖш№ЬПЯ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬ТСЦӘ
Ј¬ТСЦӘ![]() ГЧЈ¬
ГЧЈ¬![]() Ј¬јЗ
Ј¬јЗ![]() Ј¬ёГИэМхөШПВМмИјЖш№ЬПЯөДЧЬіӨ¶ИОӘ
Ј¬ёГИэМхөШПВМмИјЖш№ЬПЯөДЧЬіӨ¶ИОӘ![]() ГЧ.
ГЧ.

ЈЁ1Ј©Ҫ«![]() ұнКҫіЙ
ұнКҫіЙ![]() өДәҜКэЈ¬ІўРҙіц
өДәҜКэЈ¬ІўРҙіц![]() өД·¶О§Ј»
өД·¶О§Ј»
ЈЁ2Ј©ЗлИ·¶Ё№ӨЧчҝУ![]() өДО»ЦГЈ¬К№ҙЛҙҰөШПВМмИјЖш№ЬПЯөДЧЬіӨ¶ИЧоРЎЈ¬ІўЗуіцЧЬіӨ¶ИөДЧоРЎЦө.
өДО»ЦГЈ¬К№ҙЛҙҰөШПВМмИјЖш№ЬПЯөДЧЬіӨ¶ИЧоРЎЈ¬ІўЗуіцЧЬіӨ¶ИөДЧоРЎЦө.
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com