
【题目】二次函数f(x)=ax2+2a是区间[﹣a,a2]上的偶函数,又g(x)=f(x﹣1),则g(0),g( ![]() ),g(3)的大小关系是( )
),g(3)的大小关系是( )
A.g( ![]() )<g(0)<g(3)
)<g(0)<g(3)
B.g(0)<g( ![]() )<g(3)??
)<g(3)??
C.g( ![]() )<g(3)<g(0)
)<g(3)<g(0)
D.g(3)<g( ![]() )<g(0)
)<g(0)
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(sinx,cosx),
=(sinx,cosx), ![]() =(sinx,k),
=(sinx,k), ![]() =(﹣2cosx,sinx﹣k).
=(﹣2cosx,sinx﹣k).
(1)当x∈[0, ![]() ]时,求|
]时,求| ![]() +
+ ![]() |的取值范围;
|的取值范围;
(2)若g(x)=( ![]() +
+ ![]() )
) ![]() ,求当k为何值时,g(x)的最小值为﹣
,求当k为何值时,g(x)的最小值为﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在R上的偶函数,当x≥0时,有f(x+3)=﹣f(x),且当x∈[0,3)时,f(x)=log4(x+1),给出下列命题:
①f(2015)>f(2014);
②函数f(x)在定义域上是周期为3的函数;
③直线x﹣3y=0与函数f(x)的图象有2个交点;
④函数f(x)的值域为[0,1).
其中不正确的命题个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的方程为y2=10x,直线l的参数方程为 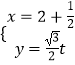 (t为参数),以坐标原点为极点,以x轴的正半轴为极轴建立极坐标系.
(t为参数),以坐标原点为极点,以x轴的正半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程和直线l的普通方程;
(2)设直线l与曲线C交于A、B两点,求弦长|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为![]() ,边界忽略不计)即为中奖·
,边界忽略不计)即为中奖·
乙商场:从装有2个白球、2个蓝球和2个红球的盒子中一次性摸出1球(这些球除颜色外完全相同),它是红球的概率是![]() ,若从盒子中一次性摸出2球,且摸到的是2个相同颜色的球,即为中奖.
,若从盒子中一次性摸出2球,且摸到的是2个相同颜色的球,即为中奖.

(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)试问:购买该商品的顾客在哪家商场中奖的可能性大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】偶函数f(x)满足f(1﹣x)=f(1+x),且在x∈[0,1]时,f(x)= ![]() ,若直线kx﹣y+k=0(k>0)与函数f(x)的图象有且仅有三个交点,则k的取值范围是 .
,若直线kx﹣y+k=0(k>0)与函数f(x)的图象有且仅有三个交点,则k的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 关于直线
关于直线![]() 对称的圆为
对称的圆为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与圆
与圆![]() 交于
交于![]() 两点,
两点, ![]() 是坐标原点,是否存在这样的直线
是坐标原点,是否存在这样的直线![]() ,使得在平行四边形
,使得在平行四边形![]() 中
中![]() ?若存在,求出所有满足条件的直线
?若存在,求出所有满足条件的直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+1(a,b∈R且a≠0),F(x)= ![]() .
.
(1)若f(﹣1)=0,且函数f(x)的值域为[0,+∞),求F(x)的解析式;
(2)在(1)的条件下,当x∈[﹣2,2]时,g(x)=f(x)﹣kx是单调函数,求实数k的取值范围;
(3)设mn<0,m+n>0,a>0,且f(x)是偶函数,判断F(m)+F(n)是否大于零.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3﹣2ax2+3x(x∈R).
x3﹣2ax2+3x(x∈R).
(1)若a=1,点P为曲线y=f(x)上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;
(2)若函数y=f(x)在(0,+∞)上为单调增函数,试求满足条件的最大整数a.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com