
°ĺŐ‚ńŅ°Ņń≥įŗľ∂∆ŕń©Ņľ ‘ļů£¨∂‘ ż—ß≥…ľ®‘ŕ![]() ∑÷“‘…Ō£®ļ¨
∑÷“‘…Ō£®ļ¨![]() ∑÷£©Ķń—ß…ķ≥…ľ®ĹÝ––Õ≥ľ∆£¨∆š∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ»ÁÕľňý ĺ.∆š÷–
∑÷£©Ķń—ß…ķ≥…ľ®ĹÝ––Õ≥ľ∆£¨∆š∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ»ÁÕľňý ĺ.∆š÷–![]() ∑÷ ż∂őĶń»ň żő™
∑÷ ż∂őĶń»ň żő™![]() »ň.
»ň.
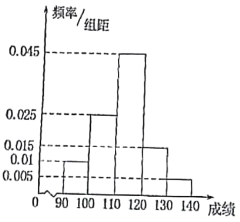
£®1£©łýĺ›∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ£¨–ī≥Ųł√įŗľ∂—ß…ķ ż—ß≥…ľ®Ķń÷ŕ ż£Ľ
£®2£©Ō÷łýĺ›—ß…ķ ż—ß≥…ľ®ī”Ķŕ“Ľ◊ťļÕĶŕňń◊ť£®ī”ĶÕ∑÷∂őĶĹłŖ∑÷∂ő“ņīőő™Ķŕ“Ľ◊ť£¨Ķŕ∂Ģ◊ť£¨![]() £¨ĶŕőŚ◊ť£©÷–»ő“‚—°≥ŲŃĹ»ň–ő≥…—ßŌį–°◊ť.»Ű—°≥ŲĶńŃĹ»ň≥…ľ®÷ģ≤Óīů”ŕ
£¨ĶŕőŚ◊ť£©÷–»ő“‚—°≥ŲŃĹ»ň–ő≥…—ßŌį–°◊ť.»Ű—°≥ŲĶńŃĹ»ň≥…ľ®÷ģ≤Óīů”ŕ![]() ∑÷‘Ú≥∆’‚ŃĹ»ňő™°į◊Óľ—◊ťļŌ°Ī£¨ ‘«ů—°≥ŲĶńŃĹ»ňő™°į◊Óľ—◊ťļŌ°ĪĶńłŇ¬ .
∑÷‘Ú≥∆’‚ŃĹ»ňő™°į◊Óľ—◊ťļŌ°Ī£¨ ‘«ů—°≥ŲĶńŃĹ»ňő™°į◊Óľ—◊ťļŌ°ĪĶńłŇ¬ .
°ĺīūįł°Ņ£®1£©÷ŕ żő™![]() £Ľ£®2£©
£Ľ£®2£©![]() .
.
°ĺĹ‚őŲ°Ņ
£®1£©łýĺ›◊ÓłŖĺō–őĶ◊ĪŖĶń÷–Ķ„÷Ķő™÷ŕ żŅ…Ķ√≥Ųīūįł£Ľ
£®2£©Ō»ľ∆ň„≥ŲĶŕ“Ľ◊ťĶń»ň żő™![]() £¨∑÷Īūľ«ő™
£¨∑÷Īūľ«ő™![]() °Ę
°Ę![]() £¨Ķŕňń◊ťĶń»ň żő™
£¨Ķŕňń◊ťĶń»ň żő™![]() £¨∑÷Īūľ«ő™
£¨∑÷Īūľ«ő™![]() °Ę
°Ę![]() °Ę
°Ę![]() £¨Ń–ĺŔ≥Ųňý”–ĶńĽýĪĺ ¬ľĢ£¨ľ« ¬ľĢ
£¨Ń–ĺŔ≥Ųňý”–ĶńĽýĪĺ ¬ľĢ£¨ľ« ¬ľĢ![]() —°≥ŲĶńŃĹ»ňő™°į◊Óľ—◊ťļŌ°Ī£¨»∑∂® ¬ľĢ
—°≥ŲĶńŃĹ»ňő™°į◊Óľ—◊ťļŌ°Ī£¨»∑∂® ¬ľĢ![]() ňýįŁļ¨ĶńĽýĪĺ ¬ľĢ£¨ņŻ”√ĻŇĶšłŇ–ÕĶńłŇ¬ Ļę ĹŅ…ľ∆ň„≥Ųňý«ů ¬ľĢĶńłŇ¬ .
ňýįŁļ¨ĶńĽýĪĺ ¬ľĢ£¨ņŻ”√ĻŇĶšłŇ–ÕĶńłŇ¬ Ļę ĹŅ…ľ∆ň„≥Ųňý«ů ¬ľĢĶńłŇ¬ .
£®1£©”…∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľŅ…÷™£¨ł√įŗľ∂—ß…ķ ż—ß≥…ľ®Ķń÷ŕ żő™![]() £Ľ
£Ľ
£®2£©Ķŕ“Ľ◊ťĶń»ň żő™![]() £¨∑÷Īūľ«ő™
£¨∑÷Īūľ«ő™![]() °Ę
°Ę![]() £¨
£¨
Ķŕňń◊ťĶń»ň żő™![]() £¨∑÷Īūľ«ő™
£¨∑÷Īūľ«ő™![]() °Ę
°Ę![]() °Ę
°Ę![]() £¨
£¨
‘ŕĶŕ“Ľ◊ťļÕĶŕňń◊ť÷–»ő“‚—°≥ŲŃĹ»ň–ő≥…—ßŌį–°◊ť£¨ňý”–ĶńĽýĪĺ ¬ľĢ”–£ļ![]() °Ę
°Ę![]() °Ę
°Ę![]() °Ę
°Ę![]() °Ę
°Ę![]() °Ę
°Ę![]() °Ę
°Ę![]() °Ę
°Ę![]() °Ę
°Ę![]() °Ę
°Ę![]() £¨Ļ≤
£¨Ļ≤![]() ÷÷£¨
÷÷£¨
ľ« ¬ľĢ![]() —°≥ŲĶńŃĹ»ňő™°į◊Óľ—◊ťļŌ°Ī£¨‘Úňý—°ĶńŃĹ»ňĪō–Ž «ņī◊‘≤ĽÕ¨ĶńŃĹ◊ť£¨
—°≥ŲĶńŃĹ»ňő™°į◊Óľ—◊ťļŌ°Ī£¨‘Úňý—°ĶńŃĹ»ňĪō–Ž «ņī◊‘≤ĽÕ¨ĶńŃĹ◊ť£¨
¬ľĢ![]() ňýįŁļ¨ĶńĽýĪĺ ¬ľĢ”–£ļ
ňýįŁļ¨ĶńĽýĪĺ ¬ľĢ”–£ļ![]() °Ę
°Ę![]() °Ę
°Ę![]() °Ę
°Ę![]() °Ę
°Ę![]() °Ę
°Ę![]() £¨Ļ≤
£¨Ļ≤![]() ÷÷£¨
÷÷£¨
“Úīň£¨![]() .
.


 √Ż–£ŅőŐ√ŌĶŃ–īūįł
√Ż–£ŅőŐ√ŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņľļ÷™÷ĪŌŖ2x©Āy©Ā1=0”Ž÷ĪŌŖx©Ā2y+1=0ĹĽ”ŕĶ„P£ģ
£®ĘŮ£©«ůĻżĶ„P«“∆Ĺ––”ŕ÷ĪŌŖ3x+4y©Ā15=0Ķń÷ĪŌŖ![]() Ķń∑Ĺ≥Ő£Ľ£®ĹŠĻŻ–ī≥…÷ĪŌŖ∑Ĺ≥ŐĶń“Ľį„ Ĺ£©
Ķń∑Ĺ≥Ő£Ľ£®ĹŠĻŻ–ī≥…÷ĪŌŖ∑Ĺ≥ŐĶń“Ľį„ Ĺ£©
£®ĘÚ£©«ůĻżĶ„P≤Ę«“‘ŕŃĹ◊ÝĪÍ÷Š…ŌĹōĺŗŌŗĶ»Ķń÷ĪŌŖ![]() ∑Ĺ≥Ő£®ĹŠĻŻ–ī≥…÷ĪŌŖ∑Ĺ≥ŐĶń“Ľį„ Ĺ£©
∑Ĺ≥Ő£®ĹŠĻŻ–ī≥…÷ĪŌŖ∑Ĺ≥ŐĶń“Ľį„ Ĺ£©
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ![]() łŲ»ňŇŇ≥…“ĽŇŇ£¨‘ŕŌ¬Ń–«ťŅŲŌ¬£¨łų”–∂ŗ…Ŕ÷÷≤ĽÕ¨ŇŇ∑®£Ņ
łŲ»ňŇŇ≥…“ĽŇŇ£¨‘ŕŌ¬Ń–«ťŅŲŌ¬£¨łų”–∂ŗ…Ŕ÷÷≤ĽÕ¨ŇŇ∑®£Ņ
£®1£©ľ◊≤Ľ‘ŕŃĹ∂ň£Ľ
£®2£©ľ◊°Ę““°ĘĪŻ»żłŲĪō–Ž‘ŕ“Ľ∆ū£Ľ
£®3£©ľ◊°Ę““Īō–Ž‘ŕ“Ľ∆ū£¨«“ľ◊°Ę““∂ľ≤Ľń‹”ŽĪŻŌŗŃŕ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨“—÷™°—OĶń÷Īĺ∂AB=3£¨Ķ„Cő™°—O…Ō“ž”ŕA£¨BĶń“ĽĶ„£¨![]() ∆Ĺ√śABC£¨«“
∆Ĺ√śABC£¨«“![]() £¨Ķ„Mő™ŌŖ∂őVBĶń÷–Ķ„.
£¨Ķ„Mő™ŌŖ∂őVBĶń÷–Ķ„.
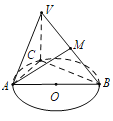
£®1£©«ů÷§£ļ![]() ∆Ĺ√śVAC£Ľ
∆Ĺ√śVAC£Ľ
£®2£©»ŰAB”Ž∆Ĺ√śVACňý≥…Ĺ«Ķń”ŗŌ“÷Ķő™![]() £¨«ů∂Ģ√śĹ«
£¨«ů∂Ģ√śĹ«![]() Ķń”ŗŌ“÷Ķ.
Ķń”ŗŌ“÷Ķ.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
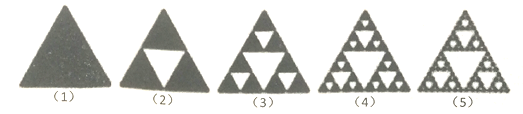
°ĺŐ‚ńŅ°Ņ–Ľ∂ŻĪŲňĻĽý»żĹ«–ő£®Sierpinski triangle£© «“Ľ÷÷∑÷–ő£¨”…≤®ņľ ż—ßľ“–Ľ∂ŻĪŲňĻĽý‘ŕ1915ńÍŐŠ≥Ų.‘ŕ“ĽłŲ’ż»żĹ«–ő÷–£¨Õ໕“ĽłŲ°į÷––ń»żĹ«–ő°Ī£®ľī“‘‘≠»żĹ«–őłųĪŖĶń÷–Ķ„ő™∂•Ķ„Ķń»żĹ«–ő£©£¨»Ľļů‘ŕ £Ō¬Ķń–°»żĹ«–ő÷–”÷Õ໕“ĽłŲ°į÷––ń»żĹ«–ő°Ī£¨ő“√«”√į◊…껿ū–őīķĪŪÕ໕Ķń≤Ņ∑÷£¨ļŕ…껿ū–őő™ £Ō¬Ķń≤Ņ∑÷£¨ő“√«≥∆īň»żĹ«–őő™–Ľ∂ŻĪŲňĻĽý»żĹ«–ő.»Ű‘ŕÕľ£®3£©ńŕňśĽķ»°“ĽĶ„£¨‘ÚīňĶ„»°◊‘–Ľ∂ŻĪŲňĻĽý»żĹ«–őĶńłŇ¬ «£® £©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°ŅŌ¬Ń–ňĶ∑®’ż»∑Ķń «£® £©
A.»Ű![]() ő™’ś√ŁŐ‚£¨‘Ú
ő™’ś√ŁŐ‚£¨‘Ú![]() £¨
£¨![]() ĺýő™ľŔ√ŁŐ‚£Ľ
ĺýő™ľŔ√ŁŐ‚£Ľ
B.√ŁŐ‚°į»Ű![]() £¨‘Ú
£¨‘Ú![]() °ĪĶńńś∑Ů√ŁŐ‚ő™’ś√ŁŐ‚£Ľ
°ĪĶńńś∑Ů√ŁŐ‚ő™’ś√ŁŐ‚£Ľ
C.Ķ»Ī» żŃ–![]() Ķń«į
Ķń«į![]() ŌÓļÕő™
ŌÓļÕő™![]() £¨»Ű°į
£¨»Ű°į![]() °Ī‘Ú°į
°Ī‘Ú°į![]() °ĪĶń∑Ů√ŁŐ‚ő™’ś√ŁŐ‚£Ľ
°ĪĶń∑Ů√ŁŐ‚ő™’ś√ŁŐ‚£Ľ
D.°į∆Ĺ√śŌÚŃŅ![]() ”Ž
”Ž![]() Ķńľ–Ĺ«ő™∂ŘĹ«°ĪĶń≥š“™ŐűľĢ «°į
Ķńľ–Ĺ«ő™∂ŘĹ«°ĪĶń≥š“™ŐűľĢ «°į![]() °Ī
°Ī
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ żf£®x£©£Ĺ£®kx+![]() £©ex©Ā2x£¨»Űf£®x£©£ľ0ĶńĹ‚ľĮ÷–”–«“÷Ľ”–“ĽłŲ’ż’Ż ż£¨‘Ú Ķ żkĶń»°÷Ķ∑∂őßő™ £®°°°°£©
£©ex©Ā2x£¨»Űf£®x£©£ľ0ĶńĹ‚ľĮ÷–”–«“÷Ľ”–“ĽłŲ’ż’Ż ż£¨‘Ú Ķ żkĶń»°÷Ķ∑∂őßő™ £®°°°°£©
A. [![]() £¨
£¨![]() £©B. £®
£©B. £®![]() £¨
£¨![]() ]
]
C. [![]() £©D. [
£©D. [![]() £©
£©
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ ż![]() .
.
£®1£©»Ű![]() £¨«ů
£¨«ů![]() Ķń÷Ķ£Ľ
Ķń÷Ķ£Ľ
£®2£©“—÷™ń≥įŗĻ≤”–![]() »ň£¨ľ«’‚
»ň£¨ľ«’‚![]() »ň…ķ»’÷Ń…Ŕ”–ŃĹ»ňŌŗÕ¨ĶńłŇ¬ ő™
»ň…ķ»’÷Ń…Ŕ”–ŃĹ»ňŌŗÕ¨ĶńłŇ¬ ő™![]() £¨
£¨![]() £¨Ĺę“ĽńÍŅī◊ų365Őž.
£¨Ĺę“ĽńÍŅī◊ų365Őž.
£®i£©«ů![]() ĶńĪŪīÔ Ĺ£Ľ
ĶńĪŪīÔ Ĺ£Ľ
£®ii£©Ļņľ∆![]() ĶńĹŁň∆÷Ķ£®ĺę»∑ĶĹ0.01£©.
ĶńĹŁň∆÷Ķ£®ĺę»∑ĶĹ0.01£©.
≤őŅľ ż÷Ķ£ļ![]() £¨
£¨![]() £¨
£¨![]() .
.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™a£ĺ0£¨«“a°Ŕ1£ģ√ŁŐ‚P£ļļĮ żf£®x£©£Ĺlogax‘ŕ£®0£¨+°ř£©…Ōő™‘ŲļĮ ż£Ľ√ŁŐ‚Q£ļļĮ żg£®x£©£Ĺx2©Ā2ax+4”–Ń„Ķ„£ģ
£®1£©»Ű√ŁŐ‚P£¨Q¬ķ◊„P’śQľŔ£¨«ů Ķ żaĶń»°÷Ķ∑∂őߣĽ
£®2£©√ŁŐ‚S£ļļĮ ży£Ĺf£®g£®x£©£©‘ŕ«Ýľš[2£¨+°ř£©…Ō÷Ķļ„ő™’ż ż£ģ»Ű√ŁŐ‚Ső™’ś√ŁŐ‚£¨«ů Ķ żaĶń»°÷Ķ∑∂őߣģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com