Question

已知射线l₁：y=4x（x≥0）和点P（6，4），试在l₁上求一点Q使得PQ所在直线l和l₁以及直线y=0在第一象限围成的面积达到最小值，并写出此时直线l的方程．

Answer 1

【答案】分析：设出点Q的坐标，写出直线PQ的方程，求出直线在x轴上的截距，然后利用三角形的面积公式列式计算面积取最大值时的a的值，则直线方程可求．
解答：解：设点Q坐标为（a，4a），PQ与x轴正半轴相交于M点．
由题意可得a＞1，否则不能围成一个三角形．
PQ所在的直线方程为：，
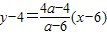
令，
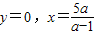
∵a＞1，∴，
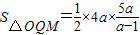
则=，
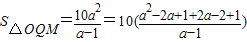
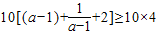
当且仅当（a-1）²=1取等号．所以a=2时，Q点坐标为（2，8）；
PQ直线方程为：x+y-10=0．
点评：本题考查了直线的图象特征与倾斜角和斜率的关系，训练了二次函数取得最值得条件，解答此题的关键是正确列出三角形面积的表达式，是中档题．