
【题目】已知椭圆Γ: ![]() +
+ ![]() =1(a>b>0)的离心率与双曲线x2﹣y2=a2的离心率之和为
=1(a>b>0)的离心率与双曲线x2﹣y2=a2的离心率之和为 ![]() ,B1、B2为椭圆Γ短轴的两个端点,P是椭圆Γ上一动点(不与B1、B2重合),直线B1P、B2P分别交直线l:y=4于M、N两点,△B1B2P的面积记为S1 , △PMN的面积记为S2 , 且S1的最大值为4
,B1、B2为椭圆Γ短轴的两个端点,P是椭圆Γ上一动点(不与B1、B2重合),直线B1P、B2P分别交直线l:y=4于M、N两点,△B1B2P的面积记为S1 , △PMN的面积记为S2 , 且S1的最大值为4 ![]() .
.
(1)求椭圆Γ的方程;
(2)若S2=λS1 , 当λ取最小值时,求点P的坐标.
【答案】
(1)
解:双曲线的离心率为 ![]() ,∴椭圆的离心率为
,∴椭圆的离心率为 ![]() ,
,
∴ 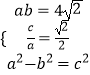 ,解得a=2
,解得a=2 ![]() ,b=2,
,b=2,
∴椭圆方程为 ![]() .
.
(2)
解:)设P(2 ![]() cosα,2sinα)(0≤α<2π且α
cosα,2sinα)(0≤α<2π且α ![]() ,α≠
,α≠ ![]() ),B1(0,2),B(0,﹣2),
),B1(0,2),B(0,﹣2),
则直线B1P的方程为y= ![]() x+2,直线B2P的方程为y=
x+2,直线B2P的方程为y= ![]() x﹣2,
x﹣2,
∴M( ![]() ,4),N(
,4),N( ![]() ,4),
,4),
|MN|=| ![]() ﹣
﹣ ![]() |=|
|=| ![]() |,
|,
∴S2= ![]() ×|MN|×(4﹣2sinα)=
×|MN|×(4﹣2sinα)= ![]() ,又S1=
,又S1= ![]() =4
=4 ![]() |cosα|,
|cosα|,
∴λ= ![]() =
= ![]() =(
=( ![]() )2,
)2,
令f(α)= ![]() ,则f′(α)=
,则f′(α)= ![]() ,
,
令f′(α)=0得α= ![]() 或α=
或α= ![]() ,
,
当0 ![]() 时,f′(α)<0,当
时,f′(α)<0,当 ![]() 时,f′(α)>0,当
时,f′(α)>0,当 ![]() 时,f′(α)>0,
时,f′(α)>0,
当 ![]() 时,f′(α)<0,当
时,f′(α)<0,当 ![]() 时,f′(α)<0,
时,f′(α)<0,
∴f(α)在[0, ![]() ]上单调递减,在(
]上单调递减,在( ![]() ,
, ![]() )上单调递增,在(
)上单调递增,在( ![]() ,
, ![]() ]上单调递增,在(
]上单调递增,在( ![]() ,
, ![]() )上单调递减,在(
)上单调递减,在( ![]() ,2π)上单调递减,
,2π)上单调递减,
∴当 ![]() 时,f(α)取得极小值f(
时,f(α)取得极小值f( ![]() )=
)= ![]() =
= ![]() ,当α=
,当α= ![]() 时,f(α)取得极大值f(
时,f(α)取得极大值f( ![]() )=
)= ![]() =﹣
=﹣ ![]() ,
,
∴当α= ![]() 或
或 ![]() 时,|f(α)|取得最小值
时,|f(α)|取得最小值 ![]() ,
,
∴λ=f2(α)的最小值为 ![]() .
.
∴当λ取得最小值时,P点坐标为( ![]() ,1)或(﹣
,1)或(﹣ ![]() ,1).
,1).
【解析】(1)根据椭圆的离心率,S1的面积列方程组,解出a,b即可得出椭圆方程;(2)设P(2 ![]() cosα,2sinα),分别求出直线方程,得出M,N的坐标,用α表示出S1 , S2 , 从而得到λ关于α的函数,利用导数判断此函数的单调性,得出λ的最小值及其对应的α,从而得出P点坐标.
cosα,2sinα),分别求出直线方程,得出M,N的坐标,用α表示出S1 , S2 , 从而得到λ关于α的函数,利用导数判断此函数的单调性,得出λ的最小值及其对应的α,从而得出P点坐标.


科目:高中数学 来源: 题型:
【题目】将函数f(x)=cos(ωx+φ)(ω>0,﹣ ![]() <φ<
<φ< ![]() )图象上每一点的横坐标伸长为原来的2倍(纵坐标不变),再向右平移
)图象上每一点的横坐标伸长为原来的2倍(纵坐标不变),再向右平移 ![]() 个单位长度得到y=cosx的图象,则函数f(x)的单调递增区间为( )
个单位长度得到y=cosx的图象,则函数f(x)的单调递增区间为( )
A.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
B.[kπ﹣ ![]() ,kπ﹣
,kπ﹣ ![]() ](k∈Z)
](k∈Z)
C.[4kπ﹣ ![]() ,kπ﹣
,kπ﹣ ![]() ](k∈Z)
](k∈Z)
D.[4kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆C1: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,x轴被曲线C2:y=x2﹣b截得的线段长等于C1的长半轴长.
,x轴被曲线C2:y=x2﹣b截得的线段长等于C1的长半轴长. 
(Ⅰ)求C1 , C2的方程;
(Ⅱ)设C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A、B,直线MA,MB分别与C1相交于D,E.
(i)证明:MD⊥ME;
(ii)记△MAB,△MDE的面积分别是S1 , S2 . 问:是否存在直线l,使得 ![]() =
= ![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的奇函数f(x)和偶函数g(x)满足f(x)=2g(x)+ ![]() ,若f(
,若f( ![]() )+f(cos2θ)<f(π)﹣f(
)+f(cos2θ)<f(π)﹣f( ![]() ),则θ的取值范围是( )
),则θ的取值范围是( )
A.(2kπ+ ![]() ,2kπ+
,2kπ+ ![]() ),k∈Z
),k∈Z
B.(2kπ﹣ ![]() ,2kπ)∪(2kπ,2kπ+π)∪(2kπ+π,2kπ+
,2kπ)∪(2kπ,2kπ+π)∪(2kπ+π,2kπ+ ![]() π),k∈Z
π),k∈Z
C.(2kπ﹣ ![]() ,2kπ﹣
,2kπ﹣ ![]() ),k∈Z
),k∈Z
D.(2kπ﹣ ![]() ,2kπ﹣π)∪(2kπ﹣π,2kπ)∪(2kπ,2kπ+
,2kπ﹣π)∪(2kπ﹣π,2kπ)∪(2kπ,2kπ+ ![]() ),k∈Z
),k∈Z
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在海岸![]() 处发现北偏东
处发现北偏东![]() 方向,距
方向,距![]() 处
处![]() 海里的
海里的![]() 处有一艘走私船.在
处有一艘走私船.在![]() 处北偏西
处北偏西![]() 方向,距
方向,距![]() 处
处![]() 海里的
海里的![]() 处的我方缉私船奉命以
处的我方缉私船奉命以![]() 海里
海里![]() 小时的速度追截走私船,此时走私船正以
小时的速度追截走私船,此时走私船正以![]() 海里
海里![]() 小时的速度从
小时的速度从![]() 处向北偏东
处向北偏东![]() 方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴的非负半轴为极轴建立极坐标系,已知曲线C:ρsin2θ=2acosθ(a>0),l: 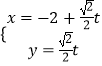 (t为参数)
(t为参数)
(1)求曲线C的普通方程,l的直角坐标方程
(2)设l与C交于M,N两点,点P(﹣2,0),若|PM|,|MN|,|PN|成等比数列,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2c﹣a)cosB﹣bcosA=0.
(Ⅰ)求角B的大小;
(Ⅱ)求 ![]() sinA+sin(C﹣
sinA+sin(C﹣ ![]() )的取值范围.
)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆C的方程为ρ=4cosθ,以极点为坐标原点,极轴为x轴的非负半轴建立平面直角坐标系,直线l经过点M(5,6),且斜率为 ![]() .
.
(1)求圆 C的平面直角坐标方程和直线l的参数方程;
(2)若直线l与圆C交于A,B两点,求|MA|+|MB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com