
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 在定义域内是增函数,且存在不相等的正实数
在定义域内是增函数,且存在不相等的正实数![]() ,使得
,使得![]() ,证明:
,证明:![]() .
.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减;
上递减;
当![]() 时,
时,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
当![]() 时,
时,![]() 在
在![]() 上递增;
上递增;
当![]() 时,
时,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
(2)证明见解析
【解析】
(1)对![]() 求导,分
求导,分![]() ,
,![]() ,
,![]() 进行讨论,可得
进行讨论,可得![]() 的单调性;
的单调性;
(2)![]() 在定义域内是是增函数,由(1)可知
在定义域内是是增函数,由(1)可知![]() ,
,![]() ,设
,设![]() ,可得
,可得![]() ,则
,则![]() ,设
,设![]() ,对
,对![]() 求导,利用其单调性可证明
求导,利用其单调性可证明![]() .
.
解:![]() 的定义域为
的定义域为![]() ,
,
因为![]() ,
,
所以![]() ,
,
当![]() 时,令
时,令 ,得
,得![]() ,令
,令 ,得
,得![]() ;
;
当![]() 时,则
时,则![]() ,令
,令 ,得
,得![]() ,或
,或![]() ,
,
令 ,得
,得![]() ;
;
当![]() 时,
时,![]() ,
,
当![]() 时,则
时,则![]() ,令
,令 ,得
,得![]() ;
;
综上所述,当![]() 时,
时,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减;
上递减;
当![]() 时,
时,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
当![]() 时,
时,![]() 在
在![]() 上递增;
上递增;
当![]() 时,
时,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
(2)![]() 在定义域内是是增函数,由(1)可知
在定义域内是是增函数,由(1)可知![]() ,
,
此时![]() ,设
,设![]() ,
,
又因为![]() ,则
,则![]() ,
,
设![]() ,则
,则
 对于任意
对于任意![]() 成立,
成立,
所以![]() 在
在![]() 上是增函数,
上是增函数,
所以对于![]() ,有
,有![]() ,
,
即![]() ,有
,有![]() ,
,
因为![]() ,所以
,所以![]() ,
,
即![]() ,又
,又![]() 在
在![]() 递增,
递增,
所以![]() ,即
,即![]() .
.


科目:高中数学 来源: 题型:
【题目】检验中心为筛查某种疾病,需要检验血液是否为阳性,对![]() 份血液样本,有以下两种检验方式:①逐份检验,需要检验
份血液样本,有以下两种检验方式:①逐份检验,需要检验![]() 次;②混合检验,即将其中
次;②混合检验,即将其中![]() (
(![]() 且
且![]() )份血液样本分别取样混合在一起检验,若检验结果为阴性,这
)份血液样本分别取样混合在一起检验,若检验结果为阴性,这![]() 份的血液全为阴性,因而这
份的血液全为阴性,因而这![]() 份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这
份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这![]() 份血液究竟哪几份为阳性,再对这
份血液究竟哪几份为阳性,再对这![]() 份再逐份检验,此时这
份再逐份检验,此时这![]() 份血液的检验次数总共为
份血液的检验次数总共为![]() 次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为![]() .
.
(1)假设有5份血液样本,其中只有2份样本为阳性,若采用逐份检验方式,求恰好经过2次检验就能把阳性样本全部检验出来的概率;
(2)现取其中![]() (
(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为点
,采用混合检验方式,样本需要检验的总次数为点![]() .当
.当![]() 时,根据
时,根据![]() 和
和![]() 的期望值大小,讨论当
的期望值大小,讨论当![]() 取何值时,采用逐份检验方式好?
取何值时,采用逐份检验方式好?
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲、乙、丙、丁、戊5种在线教学软件,若某学校要从中随机选取3种作为教师“停课不停学”的教学工具,则其中甲、乙、丙至多有2种被选取的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知f(x)=x3+3ax2+bx+a2在x=-1时有极值0,求常数a,b的值;
(2)设函数g(x)=x3-6x+5,x∈R. 若关于x的方程g(x)=m有三个不同的实根,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着运动app和手环的普及和应用,在朋友圈、运动圈中出现了每天1万步的健身打卡现象,“日行一万步,健康一辈子”的观念广泛流传.“健步达人”小王某天统计了他朋友圈中所有好友(共500人)的走路步数,并整理成下表:
分组(单位:千步) |
|
|
|
|
|
|
|
|
频数 | 60 | 240 | 100 | 60 | 20 | 18 | 0 | 2 |
(1)请估算这一天小王朋友圈中好友走路步数的平均数(同一组中数据以这组数据所在区间中点值作代表);
(2)若用![]() 表示事件“走路步数低于平均步数”,试估计事件
表示事件“走路步数低于平均步数”,试估计事件![]() 发生的概率;
发生的概率;
(3)若称每天走路不少于8千步的人为“健步达人”,小王朋友圈中岁数在40岁以上的中老年人共有300人,其中健步达人恰有150人,请填写下面![]() 列联表.根据列联表判断,有多大把握认为,健步达人与年龄有关?
列联表.根据列联表判断,有多大把握认为,健步达人与年龄有关?
健步达人 | 非健步达人 | 合计 | |
40岁以上 | |||
不超过40岁 | |||
合计 |
附: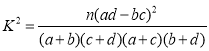 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 为抛物线
为抛物线![]() 上不同的两点,且
上不同的两点,且![]() ,点
,点![]()
![]() 且
且![]() 于点
于点![]() .
.
(1)求![]() 的值;
的值;
(2)过![]() 轴上一点
轴上一点 ![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,
两点,![]() 在
在![]() 的准线上的射影分别为
的准线上的射影分别为![]() ,
,![]() 为
为![]() 的焦点,若
的焦点,若![]() ,求
,求![]() 中点
中点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直角坐标系xOy中,椭圆![]() (a>b>0)的短轴长为
(a>b>0)的短轴长为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆的方程;
(2)斜率为1且经过椭圆的右焦点的直线交椭圆于P1、P2两点,P是椭圆上任意一点,若![]() (λ,μ∈R),证明:λ2+μ2为定值.
(λ,μ∈R),证明:λ2+μ2为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com