
已知中心为 的正方形
的正方形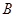 的边长为2,点
的边长为2,点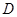 分别为线段
分别为线段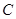 上的两个不同点,且
上的两个不同点,且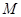 ,则
,则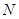 的取值范围是 .
的取值范围是 .
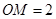
【解析】
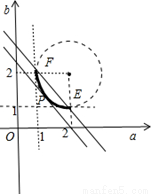
试题分析:解:如图所示,建立平面直角坐标系.设M(2,b),N(a,2).∵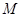 |∴
|∴ =1,即(a-2)2+(b-2)2=1.且1≤a≤2,1≤b≤2.又O(1,1),∴
=1,即(a-2)2+(b-2)2=1.且1≤a≤2,1≤b≤2.又O(1,1),∴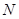 =(1,b-1)?(a-1,1)=a+b-2.令a+b-2=t,则目标函数b=-a+2+t,作出可行域(a-2)2+(b-2)2="1,"
1≤a≤2,1≤b≤2,如图2,其可行域是
=(1,b-1)?(a-1,1)=a+b-2.令a+b-2=t,则目标函数b=-a+2+t,作出可行域(a-2)2+(b-2)2="1,"
1≤a≤2,1≤b≤2,如图2,其可行域是 圆弧.①当目标函数与圆弧相切与点P时,
圆弧.①当目标函数与圆弧相切与点P时, =1,解得t=2-
=1,解得t=2-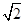 取得最小值;②当目标函数经过点EF时,t=2+1-2=1取得最大值.∴t∈[2-
取得最小值;②当目标函数经过点EF时,t=2+1-2=1取得最大值.∴t∈[2-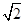 ,1].即为
,1].即为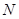 的取值范围.
的取值范围.
故答案为[2-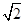 ,1].
,1].
考点:向量的模
点评:本题综合考查了向量的模的计算公式、线性规划等基础知识,及数形结合思想方法.熟练掌握是解题的关键


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010年北京市海淀区高三查漏补缺数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com