Question

已知正六棱柱的12个顶点都在一个半径为3的球面上，当正六棱柱的体积最大（柱体体积=底面积高）时，其高的值为（    ）

    A．         B．   C．        D．

 

Answer 1

【答案】

B

【解析】本题在空间几何体、导数的应用交汇处命制，解题的关键是建立正六棱柱体积的函数关系式。考生如果对选修系列四的《不等式选讲》较为熟悉的话，求函数的条件可以使用三个正数的均值不等式进行，

即，等号成立的条件是，即。根据正六棱柱和球的对称性，球心必然是正六棱柱上下底面中心连线的中点，作出轴截面即可得到正六棱柱的底面边长、高和球的半径的关系，在这个关系下求函数取得最值的条件即可求出所要求的量。

解：以正六棱柱的最大对角面作截面，如图。设球心为，正六棱柱的上下底面中心分别为，则是的中点。设正六棱柱的底面边长为，高为，则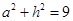。正六棱柱的体积为，即，则，得极值点，不难知道这个极值点是极大值点，也是最大值点。故当正六棱柱的体积最大，其高为。