
【题目】作出下列函数的大致图像,并写出函数的单调区间和值域:
(1)![]() ; (2)
; (2)![]() ;(3)
;(3)![]() ;
;
(4)![]() ;(5)
;(5)![]() ;(6)
;(6)![]() .
.
【答案】(1)减区间:![]() 和
和![]() ,值域:
,值域:![]() ;(2)减区间:
;(2)减区间:![]() 和
和![]() ,增区间:
,增区间:![]() 和
和![]() ,值域:
,值域:![]() ;(3)增区间:
;(3)增区间:![]() ,值域:R;(4)增区间:
,值域:R;(4)增区间:![]() 和
和![]() ,减区间:
,减区间:![]() ,值域:
,值域:![]() ;(5)减区间:
;(5)减区间:![]() 和
和![]() ,增区间:
,增区间:![]() 和
和![]() ,值域:
,值域:![]() ;(6)减区间:
;(6)减区间:![]() 和
和![]() ,增区间:
,增区间:![]() 和
和![]() ,值域:
,值域:![]() ,大致图像见解析
,大致图像见解析
【解析】
分别画出函数的图象,根据图象即可得到函数的单调区间和值域.
(1)![]() ,图象如图所示:
,图象如图所示:
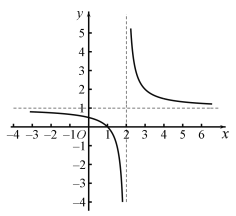
函数在![]() 和
和![]() 为减函数.
为减函数.
因为![]() ,所以
,所以![]() ,故值域为:
,故值域为:![]() ;
;
(2)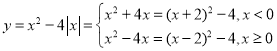 ,图象如图所示:
,图象如图所示:
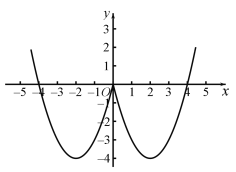
函数在![]() 和
和![]() 为减函数,在
为减函数,在![]() 和
和![]() 为增函数,
为增函数,
当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,故值域:
,故值域:![]() ;
;
(3)函数![]() 的图象如图所示:
的图象如图所示:
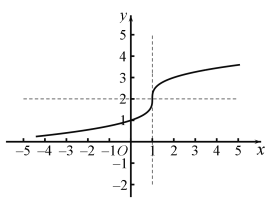
函数在![]() 上为增函数,值域:
上为增函数,值域:![]() .
.
(4)![]() ,图象如图所示:
,图象如图所示:
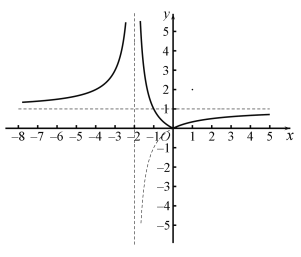
函数在![]() 和
和![]() 为增函数,在
为增函数,在![]() 为减函数,
为减函数,
值域为:![]() .
.
(5)![]() ,图象如图所示:
,图象如图所示:
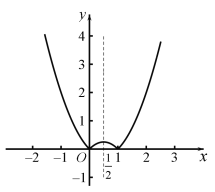
函数在![]() 和
和![]() 为减函数,在
为减函数,在![]() 和
和![]() 为增函数.
为增函数.
值域为:![]() ;
;
(6)![]()
,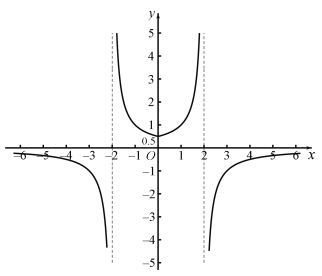
函数在![]() 和
和![]() 为减函数,在
为减函数,在![]() 和
和![]() 为增函数,
为增函数,
值域为:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足:![]()
(1) 证明:数列![]() 是等比数列;
是等比数列;
(2) 求使不等式![]() 成立的所有正整数m、n的值;
成立的所有正整数m、n的值;
(3) 如果常数0 < t < 3,对于任意的正整数k,都有![]() 成立,求t的取值范围.
成立,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
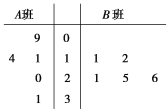
【题目】某校为了解A,B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
(1) 试估计哪个班级学生平均上网的时间较长。
(2)从A班的样本数据中随机抽取一个不超过19的数据记为a,从B班的样本数据中随机抽取一个不超过21的数据记为b,求a>b的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店为了解气温对某产品销售量的影响,随机记录了该商店![]() 月份中
月份中![]() 天的日销售量
天的日销售量![]() (单位:千克)与该地当日最低气温
(单位:千克)与该地当日最低气温![]() (单位:℃)的数据,如表所示:
(单位:℃)的数据,如表所示:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 与
与![]() 的回归方程
的回归方程![]() :
:
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地
之间是正相关还是负相关;若该地![]() 月份某天的最低气温为
月份某天的最低气温为![]() ,请用(1)中的回归方程预测该商店当日的销售量.
,请用(1)中的回归方程预测该商店当日的销售量.
参考公式: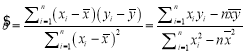 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程
的极坐标方程![]() .
.
(1)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与
与![]() 轴的两个交点分别为
轴的两个交点分别为![]() ,与
,与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,求直线
,求直线![]() 将
将![]() 分成的两部分的面积比.
分成的两部分的面积比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com