
思路分析:建立适当坐标系,设定点的坐标,然后根据已知条件列关系式求解.
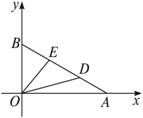
解:以直角三角形的两直角边为坐标轴,如图所示,建立直角坐标系.设A(a,0),B(0,b),D、E分别为AB的三等分点.把D点看成分![]() 成定比为λ=
成定比为λ=![]() 的定比分点,由定比分点坐标公式,可求得
的定比分点,由定比分点坐标公式,可求得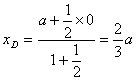 ,
,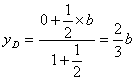 ,即D(
,即D(![]() ,
,![]() ).
).
同理可求得E(![]() ,
,![]() ).
).
又∵|OD|=sinα,|OE|=cosα,
即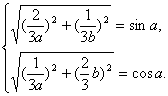
∴![]() (a2+b2)=1.
(a2+b2)=1.
又∵|AB|=![]() ,∴|AB|=
,∴|AB|=![]() .
.
方法归纳 在平面上,线段的长度通常用两点间的距离公式来表示.因此,如何建立适当的坐标系,把平面内的点用坐标表示出来成为解决几何问题的关键,而线段的定比分点坐标公式可沟通不同坐标之间的联系,故用好该公式可帮助我们更好地解决问题.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源:山西省大同一中2011-2012学年高二上学期期中考试数学试题 题型:013
给出下列命题:①底面多边形内接于一个圆的棱锥的侧棱长相等;②棱台的各侧棱不一定相交于一点;③如果不在同一平面内的两个相似的直角三角形的对应边互相平行,则连结它们的对应顶点所围成的多面体是三棱台;④圆台上底圆周上任一点与下底圆周上任一点的连线都是圆台的母线.其中正确的个数为
3
2
1
0
查看答案和解析>>
科目:高中数学 来源:训练必修二数学人教A版 人教A版 题型:013
给出下列命题:①底面多边形内接于一个圆的棱锥的侧棱长相等,②棱台的各侧棱不一定相交于一点,③如果不在同一平面内的两个相似的直角三角形的对应边互相平行,则连结它们的对应顶点所围成的多面体是三棱台,④圆台上底圆周上任一点与下底圆周上任一点的连线都是圆台的母线.其中正确的个数为
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
给出下列命题:
①底面多边形内接于一个圆的棱锥的侧棱长相等,
②棱台的各侧棱不一定相交于一点,
③如果不在同一平面内的两个相似的直角三角形的对应边互相平行,则连结它们的对应顶点所围成的多面体是三棱台,
④圆台上底圆周上任一点与下底圆周上任一点的连线都是圆台的母线.
其中正确的个数为
查看答案和解析>>
科目:高中数学 来源: 题型:
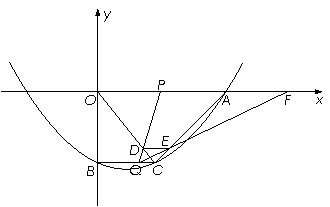
如图,在平面直角坐标系xoy中,抛物线y=![]() x 2-
x 2-![]() x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
(1)求A,B,C三点的坐标和抛物线的顶点坐标;
(2)当t为何值时,四边形PQCA为平行四边形?请写出计算过程;
(3)当t∈(0,![]() )时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;
)时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?请写出解答过程.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com