
【题目】已知函数f(x)= ![]() 是定义在(﹣1,1)上的奇函数,且f(
是定义在(﹣1,1)上的奇函数,且f( ![]() )=
)= ![]() ,则不等式f(t﹣1)+f(t)<0的解集为( )
,则不等式f(t﹣1)+f(t)<0的解集为( )
A.(0,1)
B.(0, ![]() ]
]
C.(0, ![]() )
)
D.( ![]() ,+∞)
,+∞)
【答案】C
【解析】解:∵函数f(x)= ![]() 是定义在(﹣1,1)上的奇函数,
是定义在(﹣1,1)上的奇函数,
∴f(0)=b=0,则f(x)= ![]() =
= ![]() ,
,
∵f( ![]() )=
)= ![]() ,
,
∴f( ![]() )=
)= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
则a=1,
则f(x)= ![]() ,
,
∵f(x)= ![]() =
= ![]() ,
,
∴当0<x<1时,y=x+ ![]() 为减函数,则f(x)=
为减函数,则f(x)= ![]() =
= ![]() 为增函数,
为增函数,
即f(x)= ![]() 在(﹣1,1)上是增函数,
在(﹣1,1)上是增函数,
由(t﹣1)+f(t)<0得(t﹣1)<﹣f(t)=f(﹣t),
则满足 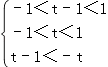 得
得 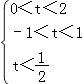 ,得0<t<
,得0<t< ![]() ,
,
即不等式的解集为(0, ![]() ),
),
故选:C
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.


 每课必练系列答案
每课必练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(1)若![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(2)令![]() ,将函数
,将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数![]() 的图象.区间
的图象.区间![]() 满足:
满足:![]() 在
在![]() 上至少含有30个零点.在所有满足上述条件的
上至少含有30个零点.在所有满足上述条件的![]() 中,求
中,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() .
.
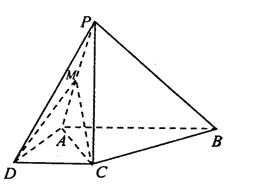
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 为线段
为线段![]() 的中点,且过
的中点,且过![]() 三点的平面与线段
三点的平面与线段![]() 交于点
交于点![]() ,确定点
,确定点![]() 的位置,说明理由;并求三棱锥
的位置,说明理由;并求三棱锥![]() 的高.
的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=loga(3﹣ax)(a>0,a≠1)
(1)当a=2时,求函数f(x)的定义域;
(2)是否存在实数a,使函数f(x)在[1,2]递减,并且最大值为1,若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?
(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2x,x∈(4,8),则函数y=f(x2)+ ![]() 的值域为( )
的值域为( )
A.[8,10)
B.( ![]() ,10)
,10)
C.(8, ![]() )
)
D.( ![]() ,10)
,10)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题P:方程x2+mx+1=0有两个不等的实数根,命题q:方程4x2+4(m﹣2)x+1=0无实数根.若p∧q为假,若p∨q为真,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动圆M与圆(x﹣1)2+y2=1相外切且与y轴相切,则动圆M的圆心的轨迹记C,
(1)求轨迹C的方程;
(2)定点A(3,0)到轨迹C上任意一点的距离|MA|的最小值;
(3)经过定点B(﹣2,1)的直线m,试分析直线m与轨迹C的公共点个数,并指明相应的直线m的斜率k是否存在,若存在求k的取值或取值范围情况[要有解题过程,没解题方程只有结论的只得结论分].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com