
【题目】已知函数![]() ,
,![]() 在
在![]() 处取极大值,在
处取极大值,在![]() 处取极小值.
处取极小值.
(1)若![]() ,求函数
,求函数![]() 的单调区间和零点个数;
的单调区间和零点个数;
(2)在方程![]() 的解中,较大的一个记为
的解中,较大的一个记为![]() ;在方程
;在方程![]() 的解中,较小的一个记为
的解中,较小的一个记为![]() ,证明:
,证明:![]() 为定值;
为定值;
(3)证明:当![]() 时,
时,![]() .
.
【答案】(1)单调增区间为![]() ;单调减区间为
;单调减区间为![]() ;3个零点(2)-1(3)见解析
;3个零点(2)-1(3)见解析
【解析】分析:(1)当![]() 时
时![]() ,求导即可得到单调区间,再利用零点存在定理判定零点即可;
,求导即可得到单调区间,再利用零点存在定理判定零点即可;
(2)因为![]() ,可知
,可知![]() . 因为
. 因为![]() ,即
,即![]() ,可知
,可知![]() ,同理,得到
,同理,得到![]() ,即可证明;
,即可证明;
(3)要证![]() ,即要证
,即要证![]() .
.
设![]() ,求导,通过单调性可知
,求导,通过单调性可知![]() ,再设
,再设![]() ,求导,通过单调性可知,
,求导,通过单调性可知,![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,且
,且![]() 和
和![]() 分别在
分别在![]() 和2.处取最大值和最小值,因此
和2.处取最大值和最小值,因此![]() 恒成立,即当
恒成立,即当![]() 时,
时,![]() .
.
解析:解(1)当![]() 时,
时,![]() ,
,![]() ;
;
当![]() 时,
时,![]() 或
或![]() ;当
;当![]() 时,
时,![]() ;
;
即函数![]() 的单调增区间为
的单调增区间为![]() ;单调减区间为
;单调减区间为![]() ;
;
又![]() ,
,![]() ,
,![]() ,
,![]() ,所以
,所以![]() 有3个零点.
有3个零点.
(2)因为![]() ,则
,则![]() ,
,
可知![]() .
.
因为![]() ,即
,即![]() ,
,
即![]()
![]() .
.
可知![]() ,
,
同理,由![]() 可知
可知
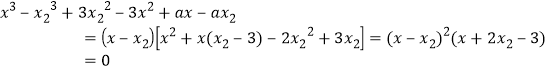 ;
;
得到![]() ;
;
![]() .
.
(3)要证![]() ,即要证
,即要证![]() .
.
设![]() ,则
,则![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
可知![]() ;
;
再设![]() ,则
,则![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
可知,![]() .
.
因为![]() ,所以
,所以![]() ,
,![]() ,且
,且![]() 和
和![]() 分别在
分别在![]() 和2处取最大值和最小值,因此
和2处取最大值和最小值,因此![]() 恒成立,即当
恒成立,即当![]() 时,
时,![]() .
.
(3)另证:一方面,易证![]() ;(略)
;(略)
另一方面,当 ![]() 时,
时,![]() ;
;
又![]() ;
;
所以,![]() ,
,
且不存在正数![]() ,使得其中等号同时成立,故
,使得其中等号同时成立,故![]() .
.


科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数![]() 是奇函数.
是奇函数.
(1)求实数a,b的值;
(2)若对任意实数x,不等式f(4x﹣k2x)+f(22x+1﹣k)<0恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某自来水厂的蓄水池有![]() 吨水,水厂每小时可向蓄水池中注水
吨水,水厂每小时可向蓄水池中注水![]() 吨,同时蓄水池又向居民小区不间断供水,
吨,同时蓄水池又向居民小区不间断供水,![]() 小时内供水总量为
小时内供水总量为![]() 吨,其中
吨,其中![]() .
.
(Ⅰ)从供水开始到第几小时,蓄水池中的存水量最少? 最少水量是多少吨?
(Ⅱ)若蓄水池中水量少于![]() 吨时,就会出现供水紧张现象,请问:在一天的
吨时,就会出现供水紧张现象,请问:在一天的![]() 小时内,大约有几小时出现供水紧张现象?
小时内,大约有几小时出现供水紧张现象?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为备战2016年奥运会,甲、乙两位射击选手进行了强化训练.现分别从他们的强化训练期间的若干次平均成绩中随机抽取8次,记录如下:
甲:8.3,9.0,7.9,7.8,9.4,8.9,8.4,8.3
乙:9.2,9.5,8.0,7.5,8.2,8.1,9.0,8.5
(1)画出甲、乙两位选手成绩的茎叶图;
(2)现要从中选派一人参加奥运会封闭集训,从统计学角度,你认为派哪位选手参加合理?简单说明理由;
(3)若将频率视为概率,对选手乙在今后的三次比赛成绩进行预测,记这三次成绩中不低于8.5分的次数为ξ,求ξ的分布列及均值E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,焦距为 2,一条准线方程为
,焦距为 2,一条准线方程为![]() ,
,![]() 为椭圆
为椭圆![]() 上一点,直线
上一点,直线![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 的坐标为
的坐标为![]() ,求过
,求过![]() 三点的圆的方程;
三点的圆的方程;
(3)若![]() ,且
,且![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.

(Ⅰ)证明: BC1//平面A1CD;
(Ⅱ)设AA1= AC=CB=2,AB=2![]() ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com