
【题目】某中学数学老师分别用两种不同教学方式对入学数学平均分和优秀率都相同的甲、乙两个高一新班(人数均为20人)进行教学(两班的学生学习数学勤奋程度和自觉性一致),数学期终考试成绩茎叶图如下:
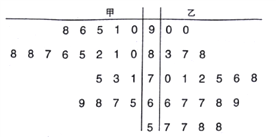
(1)学校规定:成绩不低于75分的为优秀,请填写下面的![]() 联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
联表,并判断有多大把握认为“成绩优秀与教学方式有关”.

附:参考公式及数据

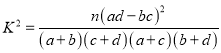
(2)从两个班数学成绩不低于90分的同学中随机抽取3名,设![]() 为抽取成绩不低于95分同学人数,求
为抽取成绩不低于95分同学人数,求![]() 的分布列和期望.
的分布列和期望.
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知某曲线C的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求该曲线C的直角坐标系方程及离心率![]()
(2)已知点![]() 为曲线C上的动点,求点
为曲线C上的动点,求点![]() 到直线
到直线![]() 的距离的最大值。
的距离的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 分别是椭圆
分别是椭圆![]()
![]()
![]() 的左、右焦点,点
的左、右焦点,点![]() 是椭圆
是椭圆![]() 上一点,且
上一点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() ,其中
,其中![]() 为坐标原点,判断
为坐标原点,判断![]() 到直线
到直线![]() 的距离是否为定值?若是,求出该定值;若不是,请说明理由.
的距离是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直.(注:
垂直.(注: ![]() 为自然对数的底数)
为自然对数的底数)
(1)求![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 上存在极值,求实数
上存在极值,求实数![]() 的取值范围;
的取值范围;
(3)求证:当![]() 时,
时, ![]() 恒成立.
恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
⑴求椭圆![]() 的标准方程;
的标准方程;
⑵已知动直线![]() 过点
过点![]() 且与椭圆
且与椭圆![]() 交于
交于![]() 两点.试问
两点.试问![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() ,过
,过![]() 、
、![]() 、
、![]() 三点的圆
三点的圆![]() 的圆心坐标为
的圆心坐标为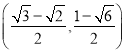 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线![]() (
(![]() 为常数,
为常数, ![]() )与椭圆
)与椭圆![]() 交于不同的两点
交于不同的两点![]() 和
和![]() .
.
(ⅰ)当直线![]() 过
过![]() ,且
,且![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(ⅱ)当坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且
,且![]() 面积为
面积为![]() 时,求直线
时,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,双曲线
,双曲线![]() 的一条渐近线与
的一条渐近线与![]() 轴所成的夹角为
轴所成的夹角为![]() ,且双曲线的焦距为
,且双曲线的焦距为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
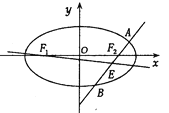
(2)设![]() 分别为椭圆
分别为椭圆![]() 的左,右焦点,过
的左,右焦点,过![]() 作直线
作直线![]() (与
(与![]() 轴不重合)交椭圆于
轴不重合)交椭圆于![]() ,
, ![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
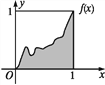
【题目】设函数y=f(x)在区间[0,1]上的图象是连续不断的一条曲线,且恒有0≤f(x)≤1,可以用随机模拟方法近似计算由曲线y=f(x)及直线x=0,x=1,y=0所围成部分的面积S.先产生两组(每组N个)0~1区间上的均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N).再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方法可得S的近似值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com